Cho tam giác nhọn ABC, các đường cao AK, BD và CE cắt nhau ở H. Gọi (O) là đường tròn đường kính AH. M là trung điểm BC. Chứng minh D và E cùng thuộc đường tròn (O)
Câu hỏi:
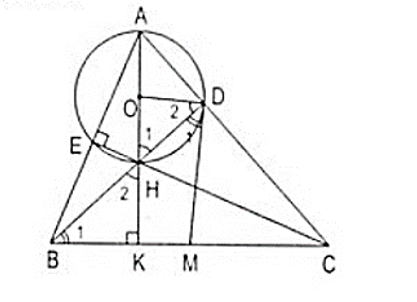
Cho tam giác nhọn ABC, các đường cao AK, BD và CE cắt nhau ở H. Gọi (O) là đường tròn đường kính AH. M là trung điểm BC.
Chứng minh D và E cùng thuộc đường tròn (O)
Trả lời:
Xét tam giác ADH, tam giác AEH lần lượt vuông tại D, E nên:
= 90° + 90° = 180°
Suy ra tứ giác ADHE nội tiếp đường tròn (O)
Mà AH là đường kính.
Vậy D, E thuộc (O) đường kính AH.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 2:
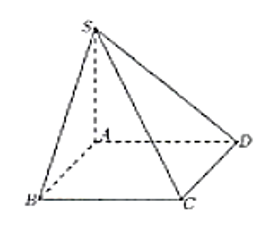
Cho hình chóp S.ABCD có đáy là hình vuông cạnh , SA vuông góc mặt phẳng đáy và SA = (minh họa hình bên). Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng?
Xem lời giải »
Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt phẳng đáy và SB = . Tính thể tích khối chóp S.ABCD?
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A, biết AC = 5 cm, AB = 6 cm và = 45°. Tính các góc , và cạnh BC (sử dụng định lí côsin)?
Xem lời giải »
Câu 6:
Cho A = 2 + 22 + 23 + … + 260. Chứng minh rằng A chia hết cho 3, 5, 7.
Xem lời giải »
Câu 8:
Tính A = (100 – 1) . (100 – 2) . . . . . (100 – 99) . (100 – 100)
Xem lời giải »