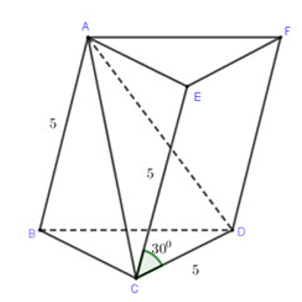
Cho tứ diện ABCD, có AB = CD = 5, khoảng cách giữa AB và CD bằng 12, góc giữa hai đường thẳng AB và CD bằng 30°. Tính thể tích khối tứ diện ABCD.

Câu hỏi:

Trả lời:

Dựng hình lăng trụ AEF.BCD

Ta có:  $V_{ABCD}=\frac{1}{3}{V}_{AEF.BCD}$ 

 $\Rightarrow V_{A.CDFE}=\frac{2}{3}{V}_{AEF.BCD}$

 $\Rightarrow V_{ABCD}=\frac{1}{2}{V}_{A.CDFE}$

Ta có: d(AB,CD) = d(AB, (CDFE)) = d(A, (CDFE))

⇒ d(A, (CDFE)) = 12

Lại có: CE = AB = CD = 5 và  $\left(\widehat{AB,CD}\right)=\left(\widehat{CE,CD}\right)=\widehat{ECD}=30°$

Nên  $S_{CDFE}=\frac{1}{3}d\left(A,\left(CDFE\right)\right).S_{CDFE}=\frac{1}{3}\cdot 12\cdot \frac{25}{2}=50$

 $V_{ABCD}=\frac{1}{2}{V}_{A.CDFE}=\frac{1}{2}.50=25$

Vậy  $V_{ABCD}=25$.