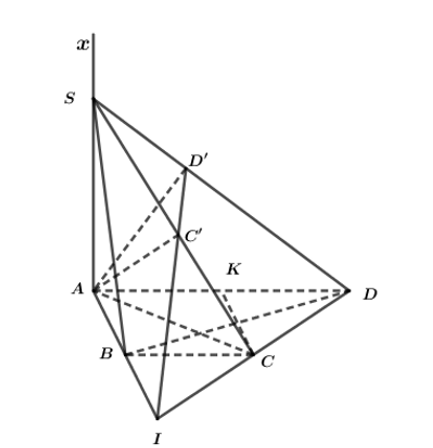
Cho hình thang ABCD vuông góc tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C’, D’ lần lượt là hình chiếu vuông góc của A trên SC và SD

Câu hỏi:

Cho hình thang ABCD vuông góc tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C’, D’ lần lượt là hình chiếu vuông góc của A trên SC và SD. Chứng minh rằng $\hat{S B C} = \hat{S C D} = 90 °$ .

Trả lời:

Ta có: SA ^ BC; AB ^ BC

Þ SB ^ BC (định lý 3 đường vuông góc) hay $\hat{S B C} = 90 °$ .

Gọi K là trung điểm của AD ta có CK = AB = AD/2 nên tam giác ACD vuông tại C

Ta có: CD ^ AC; CD ^ SA

Þ CD ^ (SAC)

Dó đó CD ^ SC hay $\hat{S C D} = 90 °$

Vậy $\hat{S B C} = \hat{S C D} = 90 °$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Tìm giao điểm 2 đường tròn (C₁): x²+ y²– 4 = 0 và (C₂): x²+ y²– 4x – 4y + 4 = 0.

Xem lời giải »

Câu 2:

Khẳng định nào sau đây sai?

Xem lời giải »

Câu 3:

Câu nào trong các câu sau không phải là mệnh đề?

Xem lời giải »

Câu 4:

Cho hình thang ABCD vuông tại A và B với $A B = B C = \frac{1}{2} A D = a$ . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành.

Xem lời giải »

Câu 5:

Cho hàm số $y = \frac{x + 2}{2 x + 3}$ (1). Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ 0.

Xem lời giải »

Câu 6:

Trong không gian Oxyz, cho điểm P(a;b;c). Tính khoảng cách từ điểm P đến trục tọa độ Oy.

Xem lời giải »

Câu 7:

Tính khoảng cách từ điểm M(−2;3;1) đến trục Ox.

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho hình thang ABCD vuông góc tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C’, D’ lần lượt là hình chiếu vuông góc của A trên SC và SD

Xem thêm bài tập Toán có lời giải hay khác: