Cho tứ diện ABCD có thể tích bằng V, hai điểm M và P lần lượt là trung điểm AB
Câu hỏi:
Cho tứ diện ABCD có thể tích bằng V, hai điểm M và P lần lượt là trung điểm AB, CD điểm N thuộc AD sao cho AD = 3AN. Tính thể tích tứ diện BMNP.
Trả lời:
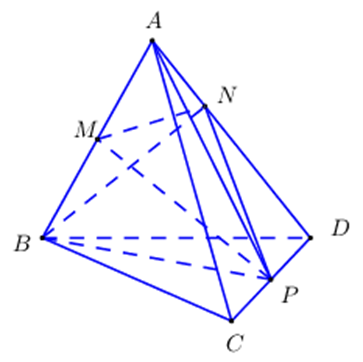
Ta có:
• \(\frac{{{V_{B.MNP}}}}{{{V_{B.ANP}}}} = \frac{{BM}}{{BA}} = \frac{1}{2} \Rightarrow {V_{B.MNP}} = \frac{1}{2}{V_{B.ANP}}\)
• \(\frac{{{S_{ANP}}}}{{{S_{ACD}}}} = \frac{{\frac{1}{2}d\left( {P,\;AD} \right)\,.\,AN}}{{\frac{1}{2}d\left( {C,\;AD} \right)\,.\,AD}} = \frac{{PD}}{{CD}} \cdot \frac{{AN}}{{AD}} = \frac{1}{2} \cdot \frac{1}{3} = \frac{1}{6}\)
\( \Rightarrow \frac{{{V_{B.ANP}}}}{{{V_{B.ACD}}}} = \frac{{{S_{ANP}}}}{{{S_{ACD}}}} = \frac{1}{6}\)
\( \Rightarrow {V_{B.ANP}} = \frac{1}{6}{V_{B.ACD}} = \frac{V}{6}\)
\( \Rightarrow {V_{B.MNP}} = \frac{1}{2}{V_{B.ANP}} = \frac{1}{2} \cdot \frac{V}{6} = \frac{V}{{12}}\).

