Cho tứ diện S.ABC có đáy là tam giác đều ABC có đường cao AH = 2a. Gọi O là trung điểm AH, SO vuông góc mp(ABC) và SO = 2a. Gọi I là một điểm trên OH, đặt AI = x (a < x < 2a) và (α) là mặt ph

Cho tứ diện S.ABC có đáy là tam giác đều ABC có đường cao AH = 2a. Gọi O là trung điểm AH, SO vuông góc mp(ABC) và SO = 2a. Gọi I là một điểm trên OH, đặt AI = x (a < x < 2a) và (α) là mặt phẳng qua I và (α) vuông góc AH.

a) Xác định thiết diện của (α) với tứ diện S.ABC.

b) Tính diện tích thiết diện của (α) và S.ABC theo a và x.

Lời giải

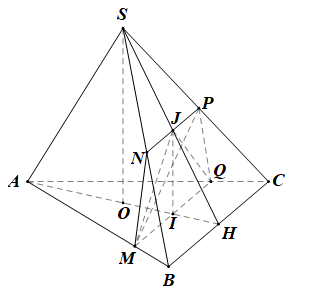
a) • Ta có: BC ⊥ OH

Qua I, dựng MQ // BC (M ∈ AB, Q ∈ AC) thì MQ ⊥ OH.

Mặt khác, ta có: SO ⊥ OH.

Dựng IJ // OS (J ∈ SH) thì IJ ∈ OH.

Do đó mp(α) là mặt phẳng (JMQ).

• Ta có: MQ // BC nên (α) // BC.

Suy ra (α) cắt (SBC) theo giao tuyến qua J và song song với BC.

Do đó, qua J dựng đường thẳng song song với BC, cắt SB và SC tại N và P ta được MNPQ là thiết diện cần dựng.

Vì NP // MQ // BC nên MNPQ là hình thang.

Ta có: OB = OC Þ DSOB = DSOC Þ SB = SC

Þ DSAB = DSAC \( \Rightarrow \widehat {SBA} = \widehat {SCA}\).

Ta cũng có: BN = CP, BM = CQ, do đó: DBMN = DCQP.

Do đó: MN = QP suy ra MP = NQ.

Vậy thiết diện là hình thang cân.

c) Do AH = 2a, ta tính được \(BC = \frac{{4a\sqrt 3 }}{3}\)

\(\frac{{MQ}}{{BC}} = \frac{{AI}}{{AH}} = \frac{x}{{2a}} \Rightarrow MQ = \frac{x}{{2a}}.\frac{{4a\sqrt 3 }}{3} = \frac{{2x\sqrt 3 }}{3}\)

\(\frac{{NP}}{{BC}} = \frac{{SJ}}{{SH}} = \frac{{OI}}{{OH}} = \frac{{x - a}}{a}\)

\( \Rightarrow NP = \frac{{x - a}}{a}.\frac{{4a\sqrt 3 }}{3} = \frac{{4\left( {x - a} \right)\sqrt 3 }}{3}\)

\(\frac{{IJ}}{{OS}} = \frac{{HI}}{{HO}} = \frac{{2a - x}}{a} \Rightarrow IJ = 2\left( {2a.x} \right)\)

\({S_{MNP}} = \frac{1}{2}\left( {MQ + NP} \right)IJ = \frac{1}{2}\left( {\frac{{2x\sqrt 3 }}{3} + \frac{{4\left( {x - a} \right)\sqrt 3 }}{3}} \right)2\left( {2a - x} \right)\)

        \( = \frac{{2\sqrt 3 }}{3}\left( {3x - 2a} \right)\left( {2a - x} \right)\).

Àp dụng bất đẳng thức Cô-si:

\(\begin{array}{*{20}{r}}{}&{S = 2\sqrt 3 \left( {x - \frac{2}{3}} \right)\left( {2a - x} \right) \le 2\sqrt 3 {{\left( {\frac{{x - - a + 2a - x}}{3}} \right)}^2} = \frac{{8\sqrt 3 }}{9}{a^2}}\end{array}\)

Dấu "=" xảy ra khi \(x.\frac{2}{3}a = 2a - x \Leftrightarrow x = \frac{4}{9}a{\rm{\;}}\left( {tm} \right)\).