Cho tứ giác ABCD (AB không song song với CD). Giả sử M, N lần lượt là trung điểm của AB và CD, thỏa mãn:
Câu hỏi:
Cho tứ giác ABCD (AB không song song với CD). Giả sử M, N lần lượt là trung điểm của AB và CD, thỏa mãn: . Chứng minh: ABCD là hình thang.
Trả lời:
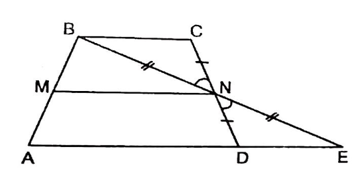
Trên tia BN lấy điểm E sao cho N là trung điểm của BE
Xét tam giác NBC và tam giác NED có:
BN = EN;
(hai góc đối đỉnh);
CN = ND (giả thiết)
Suy ra ∆NBC = ∆NED (c.g.c)
Do đó DE = BC (hai cạnh tương ứng) và (hai góc tương ứng)
Mà hai góc và ở vị trí so le trong, suy ra BC // DE
Ta có:
Xét tam giác ABE có M, N là trung điểm của AB, BE
Suy ra MN là đường trung bình của tam giác ABE
Do đó MN // AE và
Mà
Suy ra DE + AD = AE
Do đó A, D, E thẳng hàng
Mà BC // DE, suy ra BD // AD
Hay ABCD là hình thang
Vậy ABCD là hình thang.

