Cho tứ giác ABCD có AD = BC. Gọi I, J lần lượt là trung điểm của các cạnh AB và CD; K, H theo thứ tự là trung điểm của hai đường chéo AC và BD. Chứng minh rằng: IJ vuông góc HK.

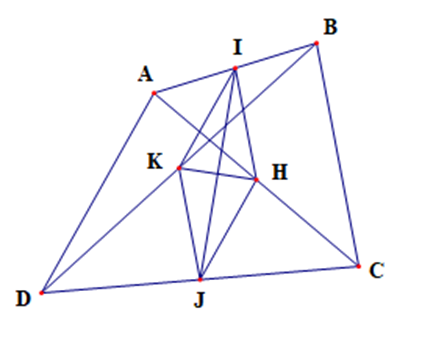
Xét tam giác ABC có IA = IB; HA = HC

Suy ra HI là đường trung bình của tam giác ABC

Do đó IH // BC và $HI=\frac{1}{2}BC$                                   (1)

Xét tam giác BDC có KD = KB; JD = JC

Suy ra KJ là đường trung bình của tam giác DBC

Do đó KJ // BC và $KJ=\frac{1}{2}BC$                                   (2)

Từ (1) va (2) suy ra KJ = IH và KJ // IH

Suy ra tứ giác KIHJ là hình bình hành

Xét tam giác ADC có HA = HC; JD = JC

Suy ra HJ là đường trung bình của tam giác ADC

Do đó $HJ=\frac{1}{2}A\text{D}$                                  

Mà AD = BC (giả thiết) và $HI=\frac{1}{2}BC$ (chứng minh trên)

Suy ra HJ = HI

Xét hình bình hành KIHJ có HJ = HI nên KIHJ là hình thoi

Mà KH và IJ là hai đường chéo nên KH ⊥ IJ

Vậy KH ⊥ IJ.