Cho tứ giác ABCD, M là một điểm nằm trong tứ giác đó. Xác định vị trí của M để MA + MB + MC + MD nhỏ nhất
Câu hỏi:
Trả lời:
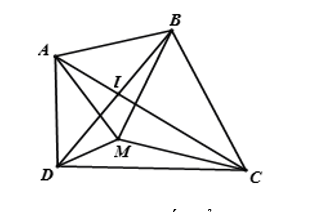
Gọi I là giao điểm của AC và BD. Ta có các bất đẳng thức:
MA + MC AC
MB + MD BD
Từ đó suy ra:
MA + MB + MC + MD AC + BD
MA + MB + MC + MD nhỏ nhất khi MA + MB + MC + MD = AC + BD khi M trùng với I.
Vậy khi M là giao điểm hai đường chéo thì MA + MB + MC + MD nhỏ nhất.

