Chứng tỏ rằng hai số 20142013 – 1 và 20142013 + 1 không thể đồng thời là hai số nguyên tố.

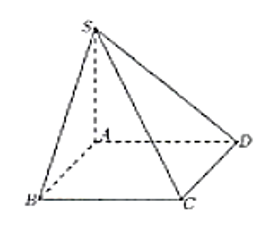
Cho hình chóp S.ABCD có đáy là hình vuông cạnh $a\sqrt{3}$, SA vuông góc mặt phẳng đáy và SA = $a\sqrt{2}$   (minh họa hình bên). Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng?

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt phẳng đáy và SB = $a\sqrt{5}$ . Tính thể tích khối chóp S.ABCD?

Cho tam giác ABC vuông tại A, biết AC = 5 cm, AB = 6 cm và = 45°. Tính các góc $\widehat{A}$ , $\widehat{C}$ và cạnh BC (sử dụng định lí côsin)?

Cho tam giác ABC vuông tại C,$\widehat{A}$ = 42°; AC = 12 cm; BC = 22 cm. Tính các cạnh và các góc của tam giác ABC.

Thực hiện phép tính: 20 – [30 – (5 – 1)²].

Thực hiện phép tính: 47 – [(45. 2⁴ – 5² . 12) : 14].

6 người thợ trong 4 giờ quét vôi được 120 m². Vậy 8 người thợ quét trong mấy giờ thì được 200 m². (Mỗi người làm sức như nhau).