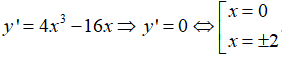GTLN của hàm số y = x^4 - 8x^2 + 16 trên đoạn [-1;3] là 0
Câu hỏi:
GTLN của hàm số trên đoạn [-1;3] là
A. 0
B. 15
C. 25
D. 30
Trả lời:
Chọn C
Xét hàm số trên đoạn [-1;3]
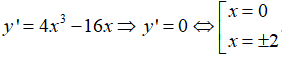
y(0) = 16, y(2) = 0; y(-1) = 9; y(3) = 25
GTLN của hàm số trên đoạn [-1;3] là 25 khi x = 3.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 2:
Giá trị lớn nhất của hàm số đạt được khi x nhận giá trị bằng
Xem lời giải »
Câu 3:
Giá trị lớn nhất của hàm số trên [0; 3] là:
Xem lời giải »
Câu 4:
Giá trị lớn nhất của hàm số có đồ thị như hình bên là
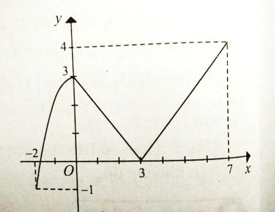
Xem lời giải »
Câu 5:
GTNN của hàm số trên nửa khoảng (-2;4] là
Xem lời giải »
Câu 6:
GTNN của hàm số trên khoảng (1; +∞) là:
Xem lời giải »
Câu 7:
GTLN của hàm số y = 2sinx + cos2x trên đoạn [0; π] là
Xem lời giải »
Câu 8:
Cho hàm số y = f(x) xác định và liên tục trên R và có bảng biến thiên. Khẳng định nào sau đây là khẳng định đúng?
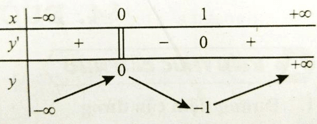
Xem lời giải »