Hàm số f(x) liên tục trên R và có đạo hàm f'(X) = x^2 (x+1)^2 (x+2)
Câu hỏi:
Hàm số f(x) liên tục trên và có đạo hàm . Phát biểu nào sau đây là đúng.
A. Hàm số đồng biến trên khoảng
B. Hàm số nghịch biến trên các khoảng và
C. Hàm số đồng biến trên khoảng
D. Hàm số đồng biến trên các khoảng và
Trả lời:
Đáp án A
Bảng xét dấu:
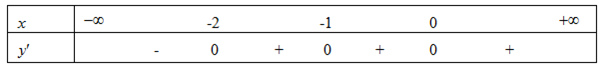
Dựa vào bảng xét dấu ta có: Hàm số đồng biến trên khoảng
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số , có đồ thị hình vẽ dưới đây. Với giá trị nào của m thì phương trình có ba nghiệm phân biệt?
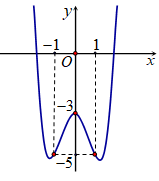
Xem lời giải »
Câu 2:
Cho hàm số y = f(x) có đồ thị (C) như hình vẽ dưới. Hỏi (C) là đồ thị của hàm số nào trong các hàm dưới đây?
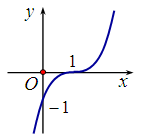
Xem lời giải »
Câu 3:
Tìm các giá trị của tham số m để hàm số đạt cực đại tại
Xem lời giải »
Câu 4:
Cho hàm số có đồ thị (C). Số tiếp tuyến của (C) song song với đường thẳng là:
Xem lời giải »
Câu 5:
Tìm giá trị thực của tham số m để hàm số đạt cực tiểu tại
Xem lời giải »
Câu 6:
Gọi S là tập hợp tất cả các giá trị của tham số nguyên m để hàm số đồng biến trên khoảng . Tập có bao nhiêu phần tử?
Xem lời giải »
Câu 7:
Giá trị của m để hàm số nghịch biến trên mỗi khoảng xác định là:
Xem lời giải »

