Câu hỏi:
Hàm số y=√4-x-√x+6 đạt giá trị nhỏ nhất tại x = x0. Tìm x0
A. x0 = -6
B. x0 = -1
C. x0 = 0
D. x0 = 4
Trả lời:
Đáp án D
Điểu kiện
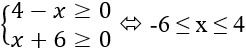
Xét -6 < x < 4, khi đó áp dụng công thức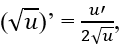 
ta có:
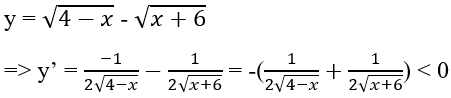
=> hàm số đã cho nghịch biến trên -6 ≤ x ≤ 4
Vì vậy, hàm số đạt giá trị nhỏ nhất tại x0 = 4
Câu 1:
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=√-x2+6x-5 trên đoạn [1;5] lần lượt là
Câu 2:
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)=2x-4√6-xtrên đoạn [-3;6]. Tổng M + m có giá trị là
Câu 3:
Hàm số y=4√x2-2x+3+2x-x2 đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là
Câu 6:
Tìm giá trị m để hai đường tiệm cận của đồ thị hàm số y=mx+23-2x( m khác -43)tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 1/5
