Phương trình |x - 2| (x + 1) + m = 0 có ba nghiệm phân biệt, giá trị thích hợp
Câu hỏi:
Phương trình \[\left| {x - 2} \right|\left( {x + 1} \right) + m = 0\] có ba nghiệm phân biệt, giá trị thích hợp của tham số m là:
A. \[0 < m < \frac{9}{4}.\]
B. 1 < m < 2.
C. \[ - \frac{9}{4} < m < 0.\]
D. ‒2 < m < 1.
Trả lời:
Đáp án đúng là: C
Xét |x − 2| (x + 1) + m = 0 (1)
Với x ≥ 2, ta có: (1) ⇔ (x − 2)(x + 1) + m = 0 ⇔ m = −x2 + x + 2
Với x<2, ta có: (1) ⇔ −(x − 2)(x + 1) + m = 0 ⇔m = x2 − x − 2
Đặt \[f\left( x \right) = \left\{ \begin{array}{l} - {x^2} + x + 2,x \ge 2\\{x^2} - x - 2,x < 2\end{array} \right.\]
Bảng biến thiên:
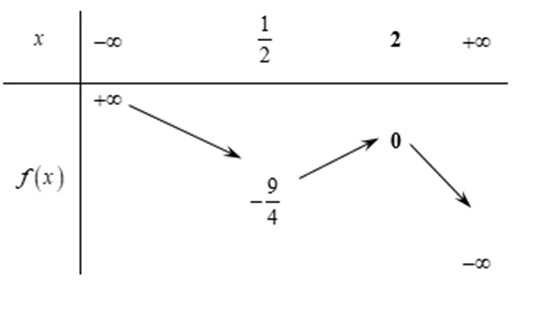
Dựa vào bảng biến thiên ta có \[ - \frac{9}{4} < m < 0.\]