Quãng đường giữa hai thành phố A và B là 120 km. Lúc 6 giờ sáng, một ô tô
Câu hỏi:
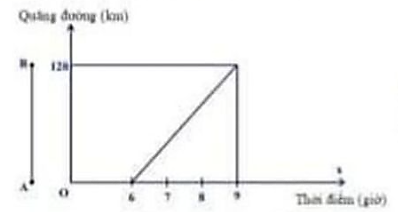
Quãng đường giữa hai thành phố A và B là 120 km. Lúc 6 giờ sáng, một ô tô xuất phát từ A đi về B. Người ta thấy mối liên hệ giữa khoảng cách của ô tô so với A và thời điểm đi của ô tô là một hàm số bậc nhất y = ax + b có đồ thị như hình sau:
a) Xác định a, b.
b) Lúc 8h sáng ô tô cách B bao nhiêu km?
Trả lời:
a) Dựa vào đồ thị ta thấy x < 6 thì y = 0
y = ax + b đi qua 2 điểm (6; 0) và (9; 120) (x ≥ 6) từ đó ta có hệ phương trình:
⇒ ⇒
Vậy a = 30, b = −240, hàm số bậc nhất là y = 40x − 240
b) Quãng đường xe đi được lúc 8 giờ sáng là:
Thay x = 8 vào hàm số bậc nhất ta có:
y = 8.40 – 240 = 80
Vậy ô tô cách A là 80km, cách B là 120 – 80 = 40km.

