Tìm các giá trị của tham số m để y = 1/3 x^3 - mx^2 + (2m -1)x - m + 2 nghịch biến
Câu hỏi:
Tìm các giá trị của tham số m để \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {2m - 1} \right)x - m + 2\) nghịch biển trên (–2; 0).
Trả lời:
Do hàm số đã cho xác định trên ℝ
y′ =x2 − 2mx + 2m − 1
Để hàm số nghịch biến trên (–2; 0)
⇒ y′ ≤ 0 ∀x ∈ (−2; 0)
⇒ x2 − 2mx + 2m – 1 ≤ 0 ∀x ∈ (−2; 0)
⇒ x2 – 1 + (2 − 2x)m ≤ 0 ∀x ∈ (−2; 0)
⇒ m ≤ \(\frac{{1 - {x^2}}}{{2 - 2x}}\)
Giả sử g(x) = \(\frac{{1 - {x^2}}}{{2 - 2x}}\)
g′(x) = \(\frac{{ - 2x\left( {2 - 2x} \right) + 2\left( {1 - {x^2}} \right)}}{{{{\left( {2 - 2x} \right)}^2}}} = \frac{{ - 4x + 4{x^2} + 2 - 2{x^2}}}{{{{\left( {2 - 2x} \right)}^2}}} = \frac{{2{{\left( {x - 1} \right)}^2}}}{{{{\left( {2 - 2x} \right)}^2}}}\)\(\)
Bảng biến thiên:
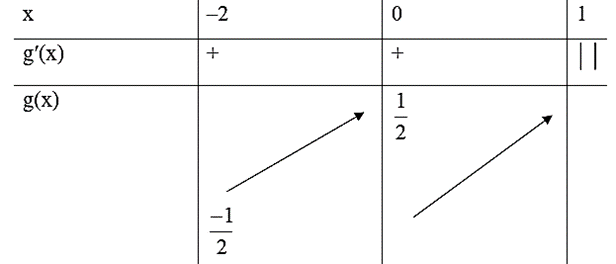
Vậy m ≤ \(\frac{{ - 1}}{2}\).