Tìm GTNN của A = x^2 – 3x + 3.

Câu hỏi:

Tìm GTNN của A = x² – 3x + 3.

Trả lời:

A = x² – 3x + 3 = $x^{2} - 2. \frac{3}{2} . x + {(\frac{3}{2})}^{2} + \frac{3}{4} = {(x - \frac{3}{2})}^{2} + \frac{3}{4}$

Vì ${(x - \frac{3}{2})}^{2} \geq 0$ với mọi x ∈ ℝ nên ${(x - \frac{3}{2})}^{2} + \frac{3}{4} \geq \frac{3}{4}$ với mọi x ∈ ℝ

Vậy GTNN của A là $\frac{3}{4}$ khi $x - \frac{3}{2} = 0$ hay x = $\frac{3}{2}$ .

Câu 1:

Cho hình thoi ABCD có cạnh bằng a và = 60°. Độ dài của vectơ $\vec{B A} + \vec{B C}$ ?

Câu 2:

Cho tam giác ABC có AB = AC và M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của NC lấy điểm K sao cho NK = NC.

a) Chứng minh ∆ABM = ∆CMA.

b) Chứng minh AK = 2MC.

c) Tính $\hat{M A K}$ .

Câu 3:

Cho tam giác ABC có AB = c, BC = a, AC = b thỏa mãn: b² + c² – a² = $\sqrt{3} b c$ . Tính số đo $\hat{B A C}$ .

Câu 4:

Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,6 cm HC = 6,4 cm.

a) Tính AB, AC, AH.

b) Kẻ HE vuông góc AB, HF vuông góc AC. Chứng minh AB.AE = AC.AF.

Câu 5:

Cho tam giác ABC vuông tại A có AB = 15, AC = 20.

a) Tính tỉ số lượng giác của B.

b) Vẽ đường cao AH. Tính độ dài các đoạn AH, HB, HC.

c) Gọi D và E lần lượt là trung điểm của BH và AH .Tia CE cắt AD tại M. Chứng minh CM =AM. cos $\hat{A C M}$ .

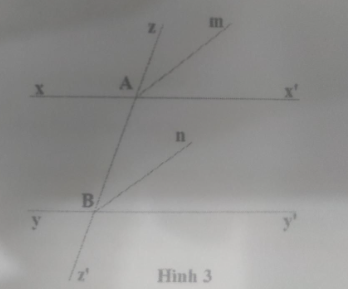
Câu 6:

Cho hình 3, biết xx' // yy' ; Am là tia phân giác của góc $\hat{z A x'}$ , Bn là tia phân giác của góc $\hat{z B y'}$ . Chứng minh Am // Bn.

Media VietJack

Câu 7:

Tìm ƯCLN (16; 40; 176).

Câu 8:

Cho tứ giác ABCD. Tìm vị trí của điểm M sao cho $\vec{M A} - \vec{M B} + \vec{A C} + \vec{M D} = \vec{C D}$

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án