Tìm m để hàm số y = x^4 – 2mx^2 + 2m + m^4 – 5 đạt cực tiểu tại x = -1
Câu hỏi:
Tìm m để hàm số y = x4 – 2mx2 + 2m + m4 – 5 đạt cực tiểu tại x = -1
A. m = -1
B. m ≠ 1
C. m = 1
D. m ≠ -1
Trả lời:
Đáp án C.
Ta có y’ = 4x3 – 4mx; y’’ = 12x2 – 4m.
Để hàm số đạt cực tiểu tại x = -1 thì y’(-1) = 0 ó -4 + 4m = 0 ó m = 1
Khi m = 1 thì y’’(-1) = 12 – 4m = 12 – 4.1 = 8 > 0 => hàm số đạt cực tiểu tại x = -1.
Vậy m = 1 là giá trị cần tìm
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [1;5] lần lượt là
Xem lời giải »
Câu 2:
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-3;6]. Tổng M + m có giá trị là
Xem lời giải »
Câu 3:
Hàm số đạt giá trị nhỏ nhất tại x = x0. Tìm x0
Xem lời giải »
Câu 4:
Hàm số đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là
Xem lời giải »
Câu 5:
Đồ thị hàm số nào sau đây có hình dạng như hình vẽ bên
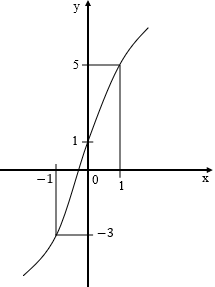
Xem lời giải »
Câu 6:
Cho hàm số y = f(x) xác định và liên tục trên đoạn [-2;2] và có đồ thị là đường cong trong hình vẽ bên. Hàm số f(x) đạt cực đại tại điểm nào dưới đây?
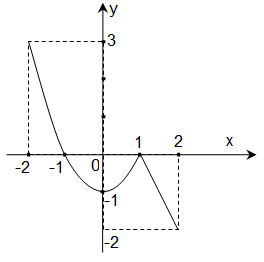
Xem lời giải »
Câu 7:
Đường cong trong hình bên là đồ thị của hàm số nào sau đây?
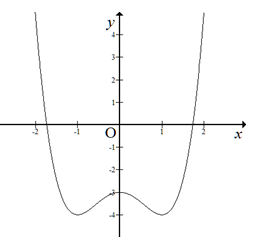
Xem lời giải »
Câu 8:
Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
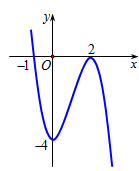
Xem lời giải »





