Tìm tất cả các giá trị thực của m để hàm số có 3 điểm cực trị
Câu hỏi:
Tìm tất cả các giá trị thực của để hàm số có 3 điểm cực trị ?
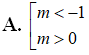
B. m < -1
C. -1 < m <0
D. m > -1.
Trả lời:
Chọn A
[Phương pháp tự luận]:
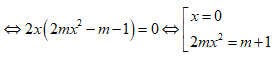
Hàm số có 3 điểm cực trị
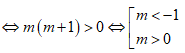
[Phương pháp trắc nghiệm] :
Đồ thị hàm số có 3 cực trị khi và chỉ khi a và b trái dấu , tức là : ab < 0
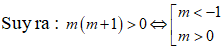
Xem thêm bài tập Toán có lời giải hay khác:
Câu 3:
Hàm số có bao nhiêu điểm cực trị?
Xem lời giải »
Câu 4:
Cho hàm số . Khẳng định nào sau đây đúng
Xem lời giải »
Câu 5:
Tìm tất cả các giá trị thực của để hàm số không có cực trị?
Xem lời giải »
Câu 6:
Tìm tất cả các giá trị thực của tham số để hàm số đạt cực đại tại ?
Xem lời giải »
Câu 7:
Cho hàm số liên tục trên R có bảng biến thiên
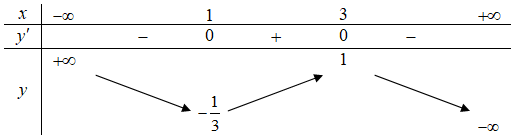
Trong các khẳng định sau, khẳng định nào là đúng?
Xem lời giải »
Câu 8:
Tìm tất cả các giá trị thực của tham số để hàm số có 2 điểm cực trị thỏa mãn .
Xem lời giải »

