Tìm tất cả các giá trị thực của tham số m sao cho

Câu hỏi:

Tìm tất cả các giá trị thực của tham số m sao cho phương trình: $\log_{3}^{2} (x) + \sqrt{\log_{3}^{2} (x) + 1} - 2 m - 1 = 0$ có ít nhất một nghiệm trên đoạn $[1; 3^{\sqrt{3}}]$ ?

A. $- 1 \leq m \leq 3$ .

B. $0 \leq m \leq 2$ .

C. $0 \leq m \leq 3$ .

D. -. $- 1 \leq m \leq 2$

Trả lời:

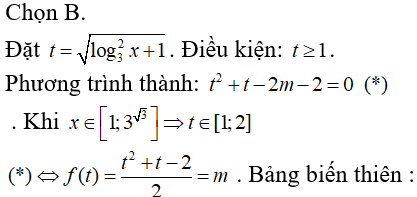
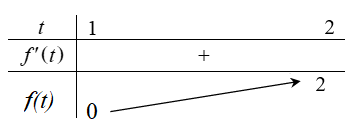
Để phương trình ban đầu có nghiệm thỏa mãn ycbt thì

phương trình f(t) = m phải có ít nhất 1 nghiệm thuộc [1; 2].

Từ bảng biến thiên ta có : $0 \leq m \leq 2$

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Tìm giá trị nhỏ nhất của tham số m sao cho hàm số $y = \frac{x^{3}}{3} + m x^{2} - m x - m$ luôn đồng biến trên $ℝ$ ?

Xem lời giải »

Câu 2:

Tìm số nguyên m nhỏ nhất sao cho hàm số $y = \frac{(m + 3) x - 2}{x + m}$ luôn nghịch biến trên các khoảng xác định của nó?

Xem lời giải »

Câu 3:

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y = \frac{m x + 4}{x + m}$ giảm trên khoảng $(- \infty; 1)$ ?

Xem lời giải »

Câu 4:

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y = x^{3} - 6 x^{2} + m x + 1$ đồng biến trên khoảng $(0; + \infty)$ ?

Xem lời giải »

Câu 5:

Tìm tất cả các giá trị thực của tham số m sao cho phương trình $\sqrt{x^{2} + m x + 2} = 2 x + 1$ có hai nghiệm thực?

Xem lời giải »

Câu 6:

Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình $3 \sqrt{x - 1} + m \sqrt{x + 1} = 2 \sqrt[4]{x^{2} - 1}$ có hai nghiệm thực?

Xem lời giải »

Câu 7:

Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình $\sqrt{(1 + 2 x) (3 - x)} > m + 2 x^{2} - 5 x - 3$ nghiệm đúng với mọi $x \in [\begin{matrix} \frac{- 1}{2}; & 3 \end{matrix}]$ ?

Xem lời giải »

Câu 8:

Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình $3 (\sqrt{1 + x} + \sqrt{3 - x}) - 2 \sqrt{(1 + x) (3 - x)} \geq m$ nghiệm đúng với mọi $x \leq [\begin{matrix} - 1; & 3 \end{matrix}]$ ?

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Tìm tất cả các giá trị thực của tham số m sao cho

Xem thêm bài tập Toán có lời giải hay khác: