Từ điểm A ở ngoài đường tròn (O; R), kẻ tiếp tuyến AB với (O) (B là tiếp điểm
Câu hỏi:
Từ điểm A ở ngoài đường tròn (O; R), kẻ tiếp tuyến AB với (O) (B là tiếp điểm). Đường thẳng đi qua B và vuông góc với OA tại H cắt (O) tại C. Vẽ đường kính BD của (O).
a) Chứng minh: AC là tiếp tuyến của (O).
b) Chứng minh: DC.OA = 2R2 .
Trả lời:
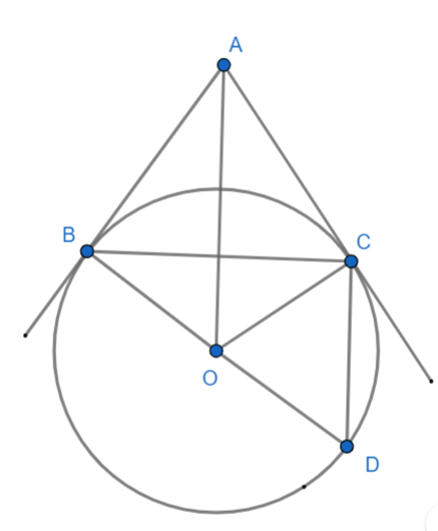
a) Xét ΔOBA và ΔOCA có:
OB = OC
\(\widehat {BOA} = \widehat {COA}\)
OA chung
Do đó: ΔOBA = ΔOCA
Suy ra: \(\widehat {OBA} = \widehat {OCA} = 90^\circ \)
Hay AC là tiếp tuyến của (O)
b) Xét (O) có
ΔBDC nội tiếp
BD là đường kính
Do đó: ΔBDC vuông tại C
Xét ΔOBA vuông tại B và ΔDCB vuông tại C có:
Do đó: ΔOBA ∽ ΔDCB.
\(\frac{{OB}}{{DC}} = \frac{{OA}}{{BD}}\)
Suy ra: DC.OA = 2R2

