Từ một điểm M nằm ngoài đường tròn (O) vẽ hai tiếp tuyến MP và MQ với đường tròn

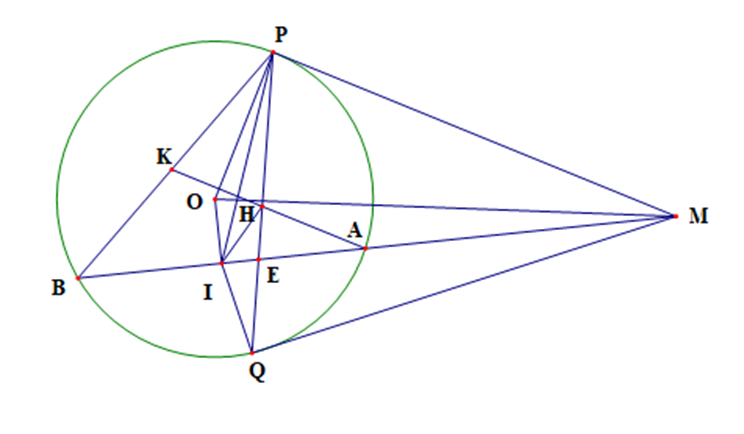
a) Vì MP, MQ là tiếp tuyến của (O) nên \(\widehat {MPO} = \widehat {MQO} = 90^\circ \)

Xét tứ giác MPOQ có \(\widehat {MPO} + \widehat {MQO} = 90^\circ + 90^\circ = 180^\circ \)

Suy ra tứ giác MPOQ nội tiếp                      (1)

Xét (O) có AB là dây cung, I là trung điểm của AB nên OI ⊥ AB

Xét tứ giác MPOI có \(\widehat {MPO} + \widehat {MIO} = 90^\circ + 90^\circ = 180^\circ \)

Suy ra tứ giác MPOI nội tiếp                        (2)

Từ (1) và (2) suy ra 5 điểm M, P, O, I, Q cùng thuộc 1 đường tròn.

b) Vì 5 điểm M, P, O, I, Q cùng thuộc 1 đường tròn nên tứ giác IPMQ nội tiếp

Suy ra \(\widehat {PIM} = \widehat {PQM} = \widehat {MPQ}\)

Xét ∆PEM và ∆IPM có

\(\widehat {EPM} = \widehat {MIP}\) (chứng minh trên)

\(\widehat {PME}\) là góc chung

Suy ra (g.g)

Do đó \(\frac{{ME}}{{PM}} = \frac{{PM}}{{IM}}\)

Suy ra MP² = ME . MI

c) Vì tứ giác IPMQ nội tiếp nên \(\widehat {IQH} = \widehat {IMP}\) (cùng chắn cung IP)

Vì AK // MP nên \(\widehat {IAH} = \widehat {IMP}\) (hai góc đồng vị)

Suy ra \(\widehat {IQH} = \widehat {IAH}\)

Do đó tứ giác AHIQ nội tiếp

Suy ra \(\widehat {AIH} = \widehat {AQH} = \widehat {QPA}\) (cùng chắn cung AI)

Mà \(\widehat {AQP} = \widehat {ABP}\) (cùng chắn cung AP)

Do đó \(\widehat {AIH} = \widehat {ABP}\), mà hai góc này ở vị trí đồng vị

Suy ra IH // BP

Xét tam giác ABK có IH // BP và \(IA = IB = \frac{1}{2}AB\)

Suy ra IH là đường trung bình

Do đó KB = 2IH.