Với mỗi số thực x, gọi f(x) là giá trị nhỏ nhất trong các số g1(x) = 4x + 1
Câu hỏi:
Với mỗi số thực x, gọi f(x) là giá trị nhỏ nhất trong các số g1(x)=4x+1,g2(x)=x+2,g3(x)=−2x+4. Giá trị lớn nhất của f(x) trên R là:
A. 13
B. 23
C. 83
D. 3
Trả lời:
Đáp án C
Quan sát các đồ thị hàm số ta thấy: (phía dưới)
+ Trong nửa khoảng (−∞;13] thì min{g1(x),g2(x),g3(x)}=g1(x) nên đồ thị hàm số y=f(x) là nửa đường thẳng y=g1(x)
+ Trong đoạn [13;23] thì min{g1(x),g2(x),g3(x)}=g2(x) nên đồ thị hàm số y=f(x) là một đoạn đường thẳng y=g2(x)
+ Trong nửa khoảng [23;+∞) thì min{g1(x),g2(x),g3(x)}=g3(x) nên đồ thị hàm số y=f(x) là nửa đường thẳng y=g3(x)
⇒ Đồ thị hàm số y=f(x) là phần đường thẳng được tô màu đỏ.
Suy ra giá trị lớn nhất của f (x) là 83
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Biết rằng đồ thị của hàm số y=P(x)=x3−2x2−5x+2 cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là x1,x2,x3. Khi đó giá trị của biểu thức T=1x21−4x1+3+1x22−4x2+3+1x23−4x3+3 bằng:
Xem lời giải »
Câu 2:
Cho hàm số y = f(x) có bảng biến thiên như sau:
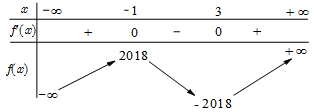
Đồ thị hàm số y=|f(x−2017)+2018| có bao nhiêu điểm cực trị?
Xem lời giải »
Câu 3:
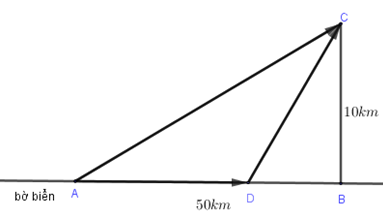
Cô An đang ở khách sạn A bên bờ biển, cô cần đi du lịch đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là 10km, khoảng cách từ khách sạn A đến điểm B trên bờ gần đảo C nhất là 50km. Từ khách sạn A, cô An có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy đến hòn đảo C (như hình vẽ). Biết rằng chi phí đi đường thủy là 5USD/km, chi phí đi đường bộ là 3USD/km. Hỏi cô An phải đi đường bộ một khoảng bao nhiêu km để chi phí là nhỏ nhất.
Xem lời giải »
Câu 4:
Tìm tập hợp S tất cả các giá trị của tham số thực m để đồ thị hàm số y=x4−2m2x2+m4+3 có ba điểm cực trị đồng thời ba điểm cực trị đó cùng với gốc tọa độ O tạo thành một tứ giác nội tiếp.
Xem lời giải »
