Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và t
Câu hỏi:
Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh.
Trả lời:
Lời giải
Gọi x là số ha đất trồng ngô, y là số ha đất trồng đậu xanh.
Ta có các điều kiện ràng buộc đối với x, y như sau:
⦁ Hiển nhiên x ≥ 0, y ≥ 0.
⦁ Diện tích canh tác không vượt quá 8 ha nên ta có x + y ≤ 8.
⦁ Số ngày công sử dụng không vượt quá 180 ngày nên 20x + 30y ≤ 180.
⇔ 2x + 3y ≤ 18.
Từ đó, ta có hệ bất phương trình mô tả các điều kiện ràng buộc là:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 8\\2x + 3y \le 18\end{array} \right.\,\,\left( * \right)\).
Yêu cầu bài toán ⇔ Tìm (x; y) thỏa (*) để F(x; y) = 40x + 50y đạt giá trị lớn nhất.
Vẽ và xác định miền nghiệm của (*):
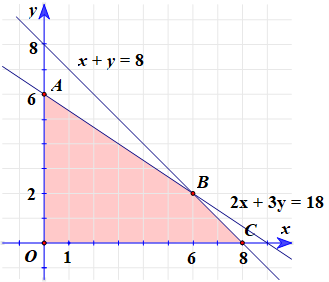
Ta có:
⦁ Miền nghiệm của (*) là tứ giác OABC (kể cả biên).
⦁ O(0; 0), A(0; 6), B(6; 2), C(8; 0).
⦁ F(O) = 0, F(A) = 300, F(B) = 340, F(C) = 320.
Suy ra maxF(x; y) = F(B) = 340 khi và chỉ khi x = 6, y = 2.
Vậy để thu được nhiều tiền nhất thì bác Năm cần trồng 6 ha ngô và 2 ha đậu xanh.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Biết rằng \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\). Tìm giá trị thực của tham số m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{1 + \cos x}}{{{{\left( {x - \pi } \right)}^2}}},\,\,\,\,\,\,x \ne \pi \\m,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \pi \end{array} \right.\) liên tục tại x = π.
Xem lời giải »
Câu 2:
Có bao nhiêu số tự nhiên nhỏ hơn 100 chia hết cho 2 và 3.
Xem lời giải »
Câu 3:
Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có sin2α + cos2α = 1.
Xem lời giải »
Câu 5:
Lớp 10B có 45 học sinh. Trong kì thi học kì I có 20 em đạt loại giỏi môn Toán; 18 em đạt loại giỏi môn Tiếng Anh; 17 em đạt loại giỏi môn Ngữ văn; 5 em đạt loại giỏi cả ba môn học trên và 7 em không đạt loại giỏi môn nào trong ba môn học trên. Số học sinh chỉ đạt loại giỏi một trong ba môn học trên là:
Xem lời giải »
Câu 6:
Trong lớp 10B có 45 học sinh, 25 học sinh thích môn Văn, 20 học sinh thích môn Toán, 18 học sinh thích môn Sử, 6 học sinh không thích môn nào, 5 học sinh thích cả 3 môn. Hỏi số học sinh chỉ thích một trong 3 môn trên?
Xem lời giải »
Câu 7:
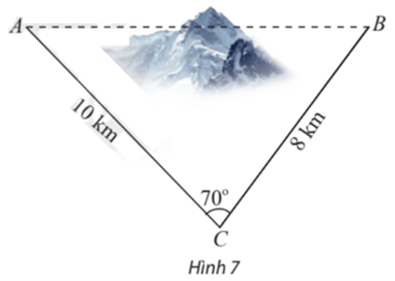
Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8 km. Góc tạo bởi hai đoạn dây AC và CB là 70°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.
Xem lời giải »
Câu 8:
Cho tứ diện đều ABCD, cạnh a. Gọi I, J lần lượt là trung điểm của AC, BC. Gọi K là một điểm trên cạnh BD sao cho KB = 2KD.
a) Xác định thiết diện của tứ diện với mặt phẳng (IJK). Chứng minh thiết diện là hình thang cân.
b) Tính diện tích thiết diện đó.
Xem lời giải »