Bác Tư du định mua một bồn nước inox hình trụ có dung tích V = 2500 lít và chiều cao h = 1,8m
Câu hỏi:
Bác Tư du định mua một bồn nước inox hình trụ có dung tích V = 2500 lít và chiều cao h = 1,8m để đựng nước. Để đưa bồn đó lên vị trí cần đặt phải qua một cửa hình chữ nhật có kích thước 1,4m × 2m. Em tính xem có thể đưa bồn đó qua cửa hình chữ nhật đó được không? Biết bán kính R của 1,8m hình tròn đáy của hình trụ được tính theo công thức R = (xem hình vē).
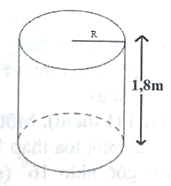
Trả lời:
V = 2500 lít = 2,5 m3
Ta có: V = Sđáy . h = πR2h
⇒ R = (m)
Đường kính d của hình tròn đáy là: d = 2R ≈ 1,33 (m)
Vì 1,33m < 1,4m và 1,8m < 2m
Nên có thể đưa bồn inox đó qua cửa hình chữ nhật.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hình thoi ABCD có cạnh bằng a và = 60°. Độ dài của vectơ ?
Xem lời giải »
Câu 2:
Cho tam giác ABC có AB = AC và M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của NC lấy điểm K sao cho NK = NC.
a) Chứng minh ∆ABM = ∆CMA.
b) Chứng minh AK = 2MC.
c) Tính .
Xem lời giải »
Câu 3:
Cho tam giác ABC có AB = c, BC = a, AC = b thỏa mãn: b2 + c2 – a2 = . Tính số đo .
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,6 cm HC = 6,4 cm.
a) Tính AB, AC, AH.
b) Kẻ HE vuông góc AB, HF vuông góc AC. Chứng minh AB.AE = AC.AF.
Xem lời giải »
Câu 5:
Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh BC. Gọi M, N theo thứ tự là hình chiếu của D tại AB, AC.
a) Chứng minh rằng: AD = MN; = 90°.
b) Gọi AH vuông góc BC tại H. Chứng minh rằng: = 90°.
c) Khi D chuyển động trên BC thì trung điểm I của MN chuyển động trên đường nào?
Xem lời giải »
Câu 6:
Lãi suất tiết kiệm 1 tháng là 0,65%. Để sau 1 tháng nhận được tiền lãi là 780000 đồng thì khách hàng phải gửi bao nhiêu tiền?
Xem lời giải »
Câu 8:
Cho tam giác ABC có G là trọng tâm. Chứng minh rằng với mọi điểm I ta có:
Xem lời giải »


