Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh BC. Gọi M, N theo thứ tự là hình chiếu của D tại AB, AC.
Câu hỏi:
Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh BC. Gọi M, N theo thứ tự là hình chiếu của D tại AB, AC.
a) Chứng minh rằng: AD = MN; = 90°.
b) Gọi AH vuông góc BC tại H. Chứng minh rằng: = 90°.
c) Khi D chuyển động trên BC thì trung điểm I của MN chuyển động trên đường nào?
Trả lời:
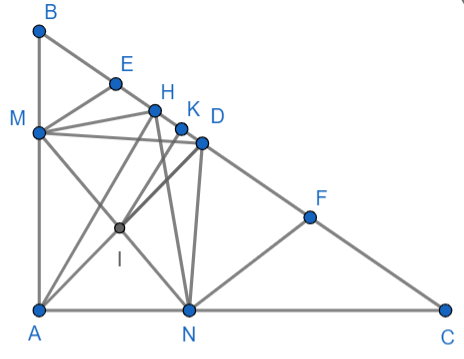
a) Ta có: = 90°
Nên AMDN là hình chữ nhật
Suy ra: AD = MN; = 90°
b) Gọi I là trung điểm của MN và AD
HI là đường trung tuyến của ∆HAD vuông tại H suy ra: HI =
Mà AD = MN nên HI =
Mà HI là đường trung tuyến của ∆HMN (I là trung điểm MN)
Nên ∆HMN vuông tại H
Suy ra: = 90°
c) Kẻ IK vuông góc HD
Ta có: AH ⊥ HD nên IK // AH
Mà I là trung điểm AD nên IK là đường trung bình của tam giác DAH
Suy ra: IK =
Điểm I cách đoạn thẳng BC 1 khoảng cố định bằng một nửa AH không đổi.
Vậy I di chuyển trên đường thẳng song song với BC và cách BC 1 khoảng bằng nửa AH.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hình thoi ABCD có cạnh bằng a và = 60°. Độ dài của vectơ ?
Xem lời giải »
Câu 2:
Cho tam giác ABC có AB = AC và M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của NC lấy điểm K sao cho NK = NC.
a) Chứng minh ∆ABM = ∆CMA.
b) Chứng minh AK = 2MC.
c) Tính .
Xem lời giải »
Câu 3:
Cho tam giác ABC có AB = c, BC = a, AC = b thỏa mãn: b2 + c2 – a2 = . Tính số đo .
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,6 cm HC = 6,4 cm.
a) Tính AB, AC, AH.
b) Kẻ HE vuông góc AB, HF vuông góc AC. Chứng minh AB.AE = AC.AF.
Xem lời giải »
Câu 5:
Lãi suất tiết kiệm 1 tháng là 0,65%. Để sau 1 tháng nhận được tiền lãi là 780000 đồng thì khách hàng phải gửi bao nhiêu tiền?
Xem lời giải »
Câu 7:
Cho tam giác ABC có G là trọng tâm. Chứng minh rằng với mọi điểm I ta có:
Xem lời giải »
Câu 8:
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6kg chất B. Từ mỗi tấn nguyên liệu loại II giá triệu đồng có thể chiết xuất được 10kg chất A và 1,5kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại
Xem lời giải »


