Cho 3 điểm A, B, C thẳng hàng và phân biệt. Trong trường hợp nào thì vectơ AB
Câu hỏi:
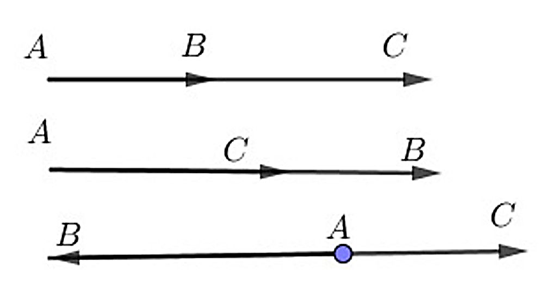
Cho 3 điểm A, B, C thẳng hàng và phân biệt. Trong trường hợp nào thì vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {AC} \)cùng hướng, trường hợp nào thì 2 vectơ đó ngược hướng.
Trả lời:
Trường hợp \(\overrightarrow {AB} \) cùng hướng với \(\overrightarrow {AC} \) khi B và C cùng nằm phía với nhau so với A.
Trường hợp \(\overrightarrow {AB} \) ngược hướng với \(\overrightarrow {AC} \) khi B và C nằm về 2 phía của A.