Cho 4 điểm A, B, C, D bất kì. a) Chứng minh: vecto DA . vecto BC + vecto DB
Câu hỏi:
Cho 4 điểm A, B, C, D bất kì.
a) Chứng minh: \[\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} = \overrightarrow 0 \].
b) Từ đó suy ra một cách chứng minh định lí: "Ba đường cao trong tam giác đồng qui".
Trả lời:
a) \[\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} \]
\[ = \overrightarrow {DA} .\left( {\overrightarrow {DC} - \overrightarrow {DB} } \right) + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} \]
\[ = \overrightarrow {DA} .\overrightarrow {DC} - \overrightarrow {DA} .\overrightarrow {DB} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} \]
\[ = \left( {\overrightarrow {DA} + \overrightarrow {AB} } \right).\overrightarrow {DC} - \left( {\overrightarrow {CA} - \overrightarrow {DA} .} \right)\overrightarrow {DB} \]
\[ = \overrightarrow {DB} .\overrightarrow {DC} - \overrightarrow {DB} .\overrightarrow {DC} \]
\[ = \overrightarrow 0 \].
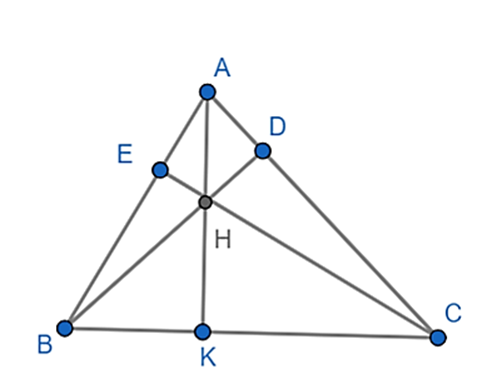
b) Xét tam giác ABC
Gọi BD và CE là đường cao của tam giác ABC
Gọi H là giao điểm của BD và CE
Theo chứng minh câu a, ta có phương trình đúng sau, với 4 điểm A,B,C,H
\[\overrightarrow {HA} .\overrightarrow {BC} + \overrightarrow {HB} .\overrightarrow {CA} + \overrightarrow {HC} .\overrightarrow {AB} = \overrightarrow 0 \]
Vì BH ⊥ AC và CH ⊥ AB nên:
\[\overrightarrow {HB} .\overrightarrow {CA} = \overrightarrow {HC} .\overrightarrow {AB} = \overrightarrow 0 \]
Do đó: \[\overrightarrow {HA} .\overrightarrow {BC} = \overrightarrow 0 \]
Suy ra: AH ⊥ BC
Vậy 3 đường cao đồng quy tại H.

