Cho 5 số thực không âm a, b, c, d, e có tổng bằng 1. Xếp 5 số này trên một đường tròn. Chứng minh rằng luôn tồn tại một cách xếp sao cho hai số bất kì cạnh nhau có tích không lớn hơn .
Câu hỏi:
Cho 5 số thực không âm a, b, c, d, e có tổng bằng 1. Xếp 5 số này trên một đường tròn. Chứng minh rằng luôn tồn tại một cách xếp sao cho hai số bất kì cạnh nhau có tích không lớn hơn .
Trả lời:
Gọi 5 số đó là a; b; c; d; e . ta có a+ b + c + d + e = 1
Không mất tính tổng quát, giả sử 0 < a < b < c < d < e
Nhận xét: c + d < . Vì nếu c + d >
Ta có: 2e > c + d > ⇒ e > ⇒ e + c + d > + = 1 .
Mâu thuẫn với a + b + c + d + e = 1 và a, b, c, d, e không âm.
Áp dụng bất đẳng thức Cô si ta có:
Mặt khác:
1 = a + b + c + d + e > a + 3b + e > 3b + e >
Suy ra:
Ta có: ae < be < ; bc < cd < ; da < dc <
Vậy có thể sắp xếp 5 số a, b, c, d, e theo thứ tự như sau: a, e, b, c, d đều thỏa mãn tích 2 số bất kì cạnh nhau không vượt quá .
Xem thêm bài tập Toán có lời giải hay khác:
Câu 2:
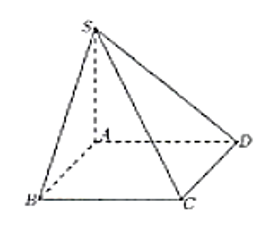
Cho hình chóp S.ABCD có đáy là hình vuông cạnh , SA vuông góc mặt phẳng đáy và SA = (minh họa hình bên). Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng?
Xem lời giải »
Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt phẳng đáy và SB = . Tính thể tích khối chóp S.ABCD?
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A, biết AC = 5 cm, AB = 6 cm và = 45°. Tính các góc , và cạnh BC (sử dụng định lí côsin)?
Xem lời giải »
Câu 5:
Tổng hai số là 46182. Hỏi sau khi thêm vào số lớn 99 đơn vị và bớt ở số bé đi 145 đơn vị thì tổng hai số đó bằng bao nhiêu?
Xem lời giải »
Câu 6:
Viết số thập phân gồm bốn trăm; sáu đơn vị; ba phần mười; hai phần nghìn.
Xem lời giải »
Câu 8:
Sắp xếp các số sau theo thứ tự từ bé đến lớ: 63817, 6035, 9872, 24655, 63298, 90909.
Xem lời giải »