Cho a, b, c khác 0 và 1/a +1/b + 1/c= 1/ a+b +c. Chứng minh (a + b)(b + c)(c + a) = 0.
Câu hỏi:
Cho a, b, c khác 0 và .
Chứng minh (a + b)(b + c)(c + a) = 0.
Trả lời:
Ta có:
⇔ (a+b+c)(ab+bc+ac)=abc
⇔ a2b + abc + a2c + ab2 + b2c + abc + abc + bc2 + ac2 = abc
⇔ (a2b + ab2) + b2c + (ac2 + bc2) + a2c + 2abc = 0
⇔ (a2b + ab2) + (b2c + abc) + (ac2 + bc2) + (a2c + abc) = 0
⇔ ab(a + b) + bc(b + a) + c2(a + b) + ac(a + b) = 0
⇔ (a + b)(ab + bc + c2 + ac) = 0
⇔ (a + b)[(ab + bc) + (c2 + ac)] = 0
⇔ (a + b)[b(a + c) + c(c + a)] = 0
⇔ (a + b)(a + c)(b + c) = 0
Vậy với a, b, c khác 0 và thì (a + b)(b + c)(c + a) = 0.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Xác định số hữu tỉ a sao cho x3 + ax2 + 5x + 3 chia hết cho x2 + 2x + 3.
Xem lời giải »
Câu 2:
Xét sự biến thiên của hàm số y = tan2x trên một chu kì tuần hoàn. Trong các kết luận sau, kết luận nào đúng?
A. Hàm số đã cho đồng biến trên khoảng và .
B. Hàm số đã cho đồng biến trên khoảng và nghịch biến trên khoảng
C. Hàm số đã cho luôn đồng biến trên khoảng .
D. Hàm số đã cho nghịch biến trên khoảng và đồng biến trên khoảng
Xem lời giải »
Câu 3:
Tìm x thỏa mãn phương trình
A. x = 2;
B. x = 4;
C. x = 1;
D. x = 3.
Xem lời giải »
Câu 6:
Cho các hàm số có đồ thị như hình vẽ
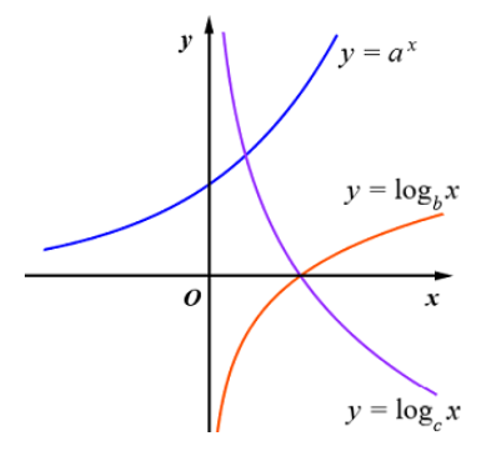
Mệnh đề nào dứoi đây đúng?
Xem lời giải »
Câu 7:
Cho a, b, c > 0. Chứng minh rằng
Xem lời giải »
Câu 8:
Cho a, b, c > 0 thỏa mãn abc = 1. Chứng minh rằng:
Xem lời giải »


