Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau. Điểm E thuộc OC, nối AE cắt (O) tại M. a) Chứng minh tứ giác OBME nội tiếp.

Câu hỏi:

Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau. Điểm E thuộc OC, nối AE cắt (O) tại M.

a) Chứng minh tứ giác OBME nội tiếp.

Trả lời:

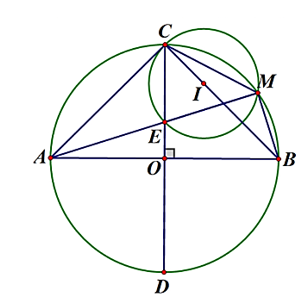
Xét đường tròn (O) có AB là đường kính, M thuộc đường tròn

$\Rightarrow \hat{A M B} = 90 ° \Rightarrow \hat{E M B} = 90 °$

Do AB vuông góc với CD nên ta có: $\hat{E O B} = 90 °$

Xét tứ giác OBME có:

$\hat{E O B} + \hat{E M B} = 90 ° + 90 ° = 180 °$

Do đó, tứ giác OBME là tứ giác nội tiếp.

Câu 1:

Chứng minh rằng mọi số tự nhiên có 3 chữ số giống nhau đều chia hết cho 37.

Câu 2:

Có bao nhiêu số lẻ có 3 chữ số mà các chữ số khác nhau ?

Câu 3:

Có bao nhiêu số có 2 chữ số đều chia hết cho cả 2 và 3.

Câu 4:

Có bao nhiêu số lẻ có 3 chữ số mà các chữ số khác nhau ?

Câu 5:

b) Chứng minh: AE.AM = AC² .

Câu 6:

c) Xác định vị trí của E để AM = 2MB.

Câu 7:

d) Gọi I là tâm đường tròn ngoại tiếp tam giác CME. Chứng minh khi E di chuyển trên OC thì I thuộc một đường thẳng cố định.

Câu 8:

Một đội công nhân có 8 người làm trong 6 ngày đắp được 360m đường. Hỏi một đội công nhân có 12 người đắp xong 1080m đường trong bao nhiêu ngày ?

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án