Cho đường tròn (O) đường kính AB. Trên tiếp tuyến Ax lấy điểm C(Ckhác A)
Câu hỏi:
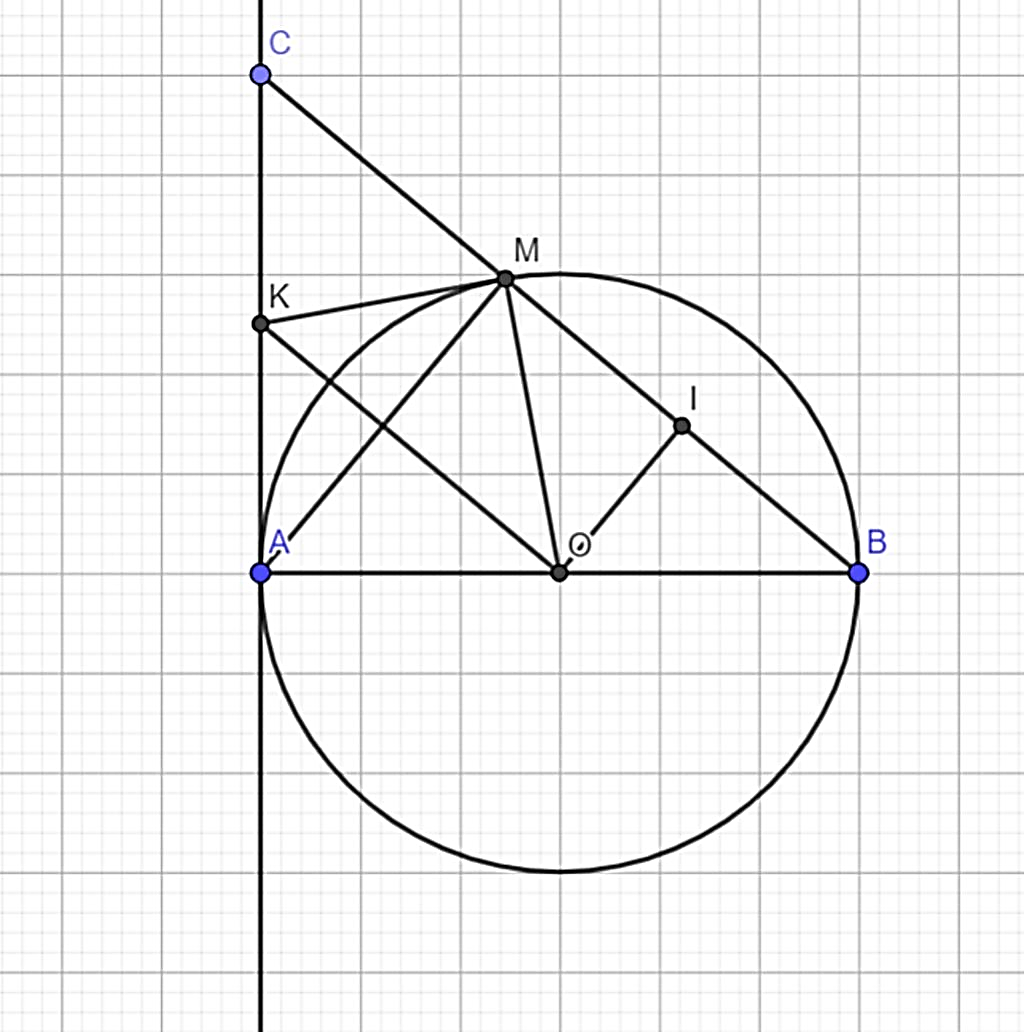
Cho đường tròn (O) đường kính AB. Trên tiếp tuyến Ax lấy điểm C(C≠ A). Đoạn thẳng BC cắt (O) tại M. Gọi I là trung điểm của MB, K là trung điểm của AC.
a) Chứng minh AM là đường cao của tam giác ABC và AC2 = CM.CB.
b) Chứng minh A, C, I, O cùng nằm trên 1 đường tròn.
c) Chứng minh KM là tiếp tuyến của đường tròn (O).
Trả lời:
Vì AB là đường kính của (O) ⇒ AM ⊥ BM
⇒ AM ⊥ BC
⇒ AM là đường cao ΔABC
Ta có AC là tiếp tuyến của (O)
⇒ AC ⊥ AB
⇒ ΔABC vuông tại Ado AM ⊥ BC
⇒ AC2 = CM.CB (Hệ thức lượng trong tam giác vuông)
b) Ta có I là trung điểm MB ⇒ OI ⊥ MB
⇒ = 90°
⇒ A, O, I, C ∈ đường tròn đường kính CO
c) Ta có O,K là trung điểm AB,AC
⇒ OK là đường trung bình ΔABC
⇒ OK//BC
⇒ OK⊥AM vì AM⊥BC
⇒ OK là trung trực của AM
⇒ M, A đối xứng qua OK
⇒ = 90°
⇒ KM là tiếp tuyến của (O).

