Cho đường tròn (O; R), đường kính AB. Vẽ dây cung BC = R. Đường thẳng qua O vuông góc với AC cắt tiếp tuyến tại A của đường tròn (O) tại D. Chứng minh DC là tiếp tuyến của đường tròn (O).

Cho đường tròn (O; R), đường kính AB. Vẽ dây cung BC = R. Đường thẳng qua O vuông góc với AC cắt tiếp tuyến tại A của đường tròn (O) tại D. Chứng minh DC là tiếp tuyến của đường tròn (O).

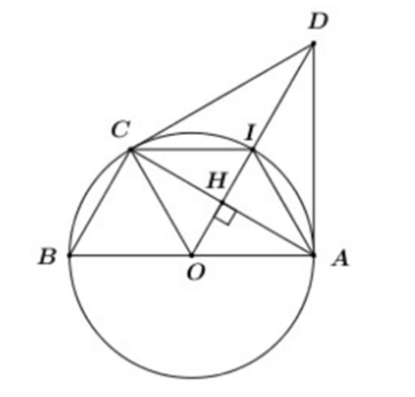
Gọi H = OD ∩ AC

Ta có: OD ⊥ AC tại H 

⇒ H là trung điểm của AC

⇒ OD là trung trực của AC

⇒ DA = DC (tính chất đường trung trực).

Xét ΔOAD và ΔOCD có:

OA = OC (= R)

OD chung

DA = DC

Þ ΔOAD = ΔOCD (c.c.c)

$\Rightarrow \widehat{OAD}=\widehat{OCD}$

Mà $\widehat{OAD}=90°$

$\Rightarrow \widehat{OCD}=90°$

Þ OC ⊥ CD

Vậy CD là tiếp tuyến của đường tròn (O) tại C.