Cho đường tròn (O; R) và 1 điểm A sao cho OA = R căn 2
Câu hỏi:
Cho đường tròn (O; R) và 1 điểm A sao cho OA = . Vẽ tiếp tuyến AB, AC với đường tròn 1 góc = 45° cắt đoạn thẳng AB và AC lần lượt tại D và E.
Chứng minh:
a) DE là tiếp tuyến của đường tròn (O).
b) .
Trả lời:
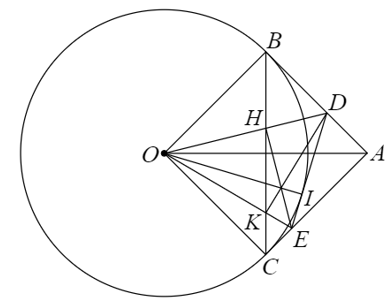
Vì OA = = OB = OC nên tứ giác ABOC là hình vuông
Suy ra = 45°, suy ra tứ giác DBOK nội tiếp
Do đó = 180° – = 90° hay DK ⊥ OE
Tương tự EH ⊥ OD.
Suy ra do DHKE nội tiếp
Suy ra DO là phân giác . Mà AO là phân giác nên O là tâm bàng tiếp góc A của ΔADE
Do vậy DE + AD + AE = 2AB = 2R
Ta có 2R = DE + AD + AE > DE + DE = 2DE ⇒ DE < R
Lại có
Vậy

