Cho đường tròn (O; R) và điểm A nằm bên ngoài đường tròn. Kẻ tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). 1. Chứng minh ABOC là tứ giác nội tiếp.
Câu hỏi:
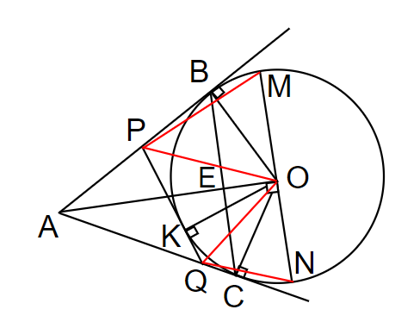
Cho đường tròn (O; R) và điểm A nằm bên ngoài đường tròn. Kẻ tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
1. Chứng minh ABOC là tứ giác nội tiếp.
Trả lời:
1)
Vì AB là tiếp tuyến (O; R) nên AB vuông góc với OB
Vì AC là tiếp tuyến (O; R) nên AC vuông góc với OC
Ta có:
Do đó, tứ giác ABOC nội tiếp đường tròn
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Chứng minh rằng mọi số tự nhiên có 3 chữ số giống nhau đều chia hết cho 37.
Xem lời giải »
Câu 2:
Có bao nhiêu số lẻ có 3 chữ số mà các chữ số khác nhau ?
Xem lời giải »
Câu 3:
Có bao nhiêu số có 2 chữ số đều chia hết cho cả 2 và 3.
Xem lời giải »
Câu 4:
Có bao nhiêu số lẻ có 3 chữ số mà các chữ số khác nhau ?
Xem lời giải »
Câu 5:
2. Gọi E là giao điểm của BC và OA. Chứng minh BE vuông góc với OA và OE.OA = R2.
Xem lời giải »
Câu 6:
3. Trên cung nhỏ BC của đường tròn (O; R) lấy điểm K bất kỳ (K khác B và C). Tiếp tuyến tại K của đường tròn (O; R) cắt AB, AC theo thứ tự tại P, Q. Chứng minh tam giác APQ có chu vi không đổi khi K chuyển động trên cung nhỏ BC.
Xem lời giải »
Câu 7:
Chứng minh rằng: Nếu p là số nguyên tố lớn hơn 3 thì (p – 1).(p + 1) chia hết cho 24.
Xem lời giải »