Cho đường tròn (O; R). Vẽ dây AB sao cho số đo của cung nhỏ AB bằng 1 1/2
Câu hỏi:
Cho đường tròn (O; R). Vẽ dây AB sao cho số đo của cung nhỏ AB bằng 1\(\frac{1}{2}\) số đo của cung lớn AB. Tính diện tích của tam giác AOB.
Trả lời:
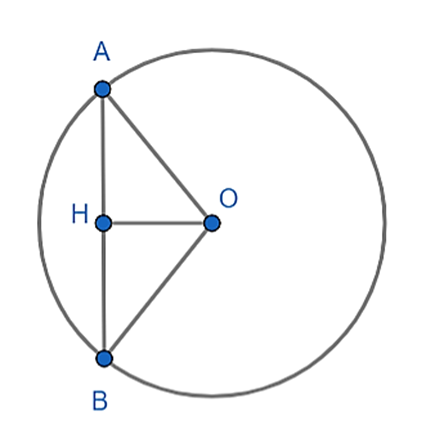
Vì sđnhỏ = \(\frac{1}{2}\)sđlớn
Suy ra: sđnhỏ = \(\frac{{360}}{3} = 120^\circ \)
Do sđnhỏ = \[\widehat {AOB} = 120^\circ \]
Xét tam giác AOB có OA = OB = R
Nên tam giác AOB cân tại O
Suy ra: \[\widehat {OAB} = \frac{{180^\circ - 120^\circ }}{2} = 30^\circ \]
Kẻ OH ⊥ AB
OH = OA.sin\[\widehat {OAB} = OA.\sin 30^\circ = R\sin 30^\circ = \frac{R}{2}\]
Diện tích tam giác AOB là: S = \(\frac{1}{2}.AB.OH = \frac{1}{2}.R\sqrt 3 .\frac{R}{2} = \frac{{{R^2}\sqrt 3 }}{4}\).

