Cho đường tròn (O; R). Vẽ hai bán kính OA, OB. Trên các bán kính OA, OB lần lượt lấy các điểm M, N sao cho OM = ON. Vẽ dây CD đi qua M, N (M nằm giữa C và N). a) Chứng minh CM = DN.
Câu hỏi:
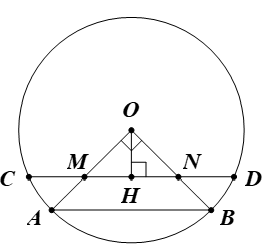
Cho đường tròn (O; R). Vẽ hai bán kính OA, OB. Trên các bán kính OA, OB lần lượt lấy các điểm M, N sao cho OM = ON. Vẽ dây CD đi qua M, N (M nằm giữa C và N).
a) Chứng minh CM = DN.
Trả lời:
a) Kẻ OH ⊥ CD (H ∈ CD).
Suy ra H là trung điểm CD.
Do đó HC = HD (quan hệ giữa đường kính và dây cung) (1)
Tam giác OMN cân tại O (do OM = ON).
Suy ra OH vừa là đường cao, vừa là đường trung tuyến của tam giác OMN.
Do đó HM = HN (2)
Lại có CH = CM + MH và DH = DN + NH (3)
Từ (1), (2), (3), suy ra CM = DN.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Một mảnh đất hình chữ nhật có chu vi 96 m, chiều dài bằng chiều rộng. Người ta đã sử dụng diện tích mảnh đất để xây nhà. Tính diện tích phần đất xây nhà.
Xem lời giải »
Câu 2:
Một sân vườn hình chữ nhật có chu vi là 64 m, chiều dài gấp 3 lần chiều rộng.
a) Tính diện tích khu vườn.
Xem lời giải »
Câu 3:
b) Người ta dự định rào khu vườn bằng lưới kẽm. Biết mỗi mét lưới kẽm giá 100 000 đồng. Tính số tiền mua lưới.
Xem lời giải »
Câu 4:
Một vườn hoa có diện tích 800 m2 nằm trong công viên có diện tích 25 ha. Hỏi diện tích vườn hoa chiếm bao nhiêu phần diện tích công viên?
Xem lời giải »
Câu 5:
b) Giả sử . Tính OM theo R sao cho CM = MN = ND.
Xem lời giải »
Câu 6:
Phân tích đa thức sau thành nhân tử: (x – y)2 + (y – z)2 + (z – x)2.
Xem lời giải »
Câu 7:
Cho (x – y)2 + (y – z)2 + (z – x)2 = 4(x2 + y2 + z2 – xy – yz – zx). Chứng minh x = y = z.
Xem lời giải »
Câu 8:
Qua đỉnh A của hình vuông ABCD cạnh bằng a, vẽ một đường thẳng cắt BC ở M và cắt DC ở I. Chứng minh .
Xem lời giải »