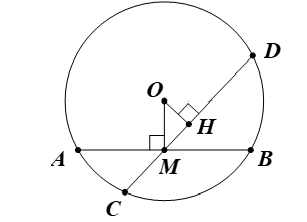
Cho đường tròn (O) và dây AB không là đường kính. Gọi M là trung điểm của AB. Qua M vẽ dây CD không trùng với AB. Chứng minh: a) M không là trung điểm của CD.

Cho hai tập hợp A = {0; 1}, B = {0; 1; 2; 3; 4}. Số tập X thỏa mãn X là con của C_AB là bao nhiêu?

Mua một tá bút chì hết 36 000 đồng. Hỏi mua 39 cái hết bao nhiêu tiền?

Chứng minh nếu n² là số chẵn thì n cũng là số chẵn.

Người ta phơi 450 kg hạt tươi thì được hạt khô. Biết tỉ lệ nước trong hạt tươi là 20%, tỉ lệ nước trong hạt khô là 10%. Tính khối lượng hạt khô.

Chứng minh:

b) AB < CD.

Thực hiện phép tính: 5³ . 7⁵ : 35.

Có hai xe ô tô, mỗi xe chở 4200 kg gạo và 3 xe ô tô, mỗi xe chở 3600 kg gạo. Trung bình mỗi xe chở số ki-lô-gam gạo là