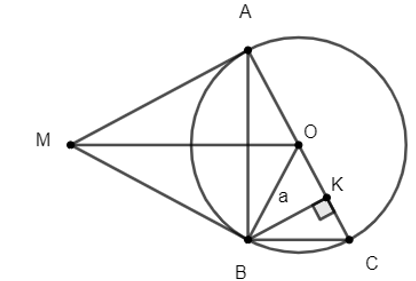
Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB tới đường tròn (O) với A, B là các tiếp điểm. a) Chứng minh bốn điểm A, B, M, O cùng thuộc một đường tròn.

Câu hỏi:

Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Qua M kẻ các tiếp tuyến MA, MB tới đường tròn (O) với A, B là các tiếp điểm.

a) Chứng minh bốn điểm A, B, M, O cùng thuộc một đường tròn.

Trả lời:

a) Xét tứ giác AOBM có:

$\hat{M A O} + \hat{M B O} = 90 ° + 90 ° = 180 °$

Do đó tứ giác AOBM là tứ giác nội tiếp đường tròn.

Vậy bốn điểm A, B, M, O cùng thuộc một đường tròn.

Câu 1:

Cho tam giác ABC vuông tại A có AB < AC. Gọi D và E lần lượt là trung điểm của các cạnh AC và BC, kẻ EF ⊥ AB tại F.

a) Chứng minh ADEF là hình chữ nhật.

Câu 2:

b) Gọi G là điểm đối xứng với E qua D. Chứng minh tứ giác AECG là hình thoi.

Câu 3:

Cho ∆ABC vuông tại A, có $\hat{C} = 30 °$ . Gọi M và N lần lượt là trung điểm của BC và AC.

a) Tính $\hat{N M C}$ .

Câu 4:

b) Gọi E là điểm đối xứng với M qua N. Chứng minh tứ giác AECM là hình thoi.

Câu 5:

b) Kẻ đường kính AC của đường tròn (O). Chứng minh OM // CB.

Câu 6:

c) Vẽ BK vuông góc với AC tại K. Chứng minh: CK.OM = OB.CB.

Câu 7:

Tính (7²⁰¹⁴ + 7²⁰¹²) : 7²⁰¹².

Câu 8:

Tìm chữ số tận cùng của 7⁹⁹.

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án