. Cho đường tròn tâm O đường kính AB = 2R. CD là đường kính di động. Gọi d là
Câu hỏi:
Cho đường tròn tâm O đường kính AB = 2R. CD là đường kính di động. Gọi d là tiếp tuyến tại B của đường tròn (O), các đường thẳng AC, AD cắt d lần lượt tại P và Q.Chứng minh tứ giác CPQD nội tiếp được đường tròn.
Trả lời:
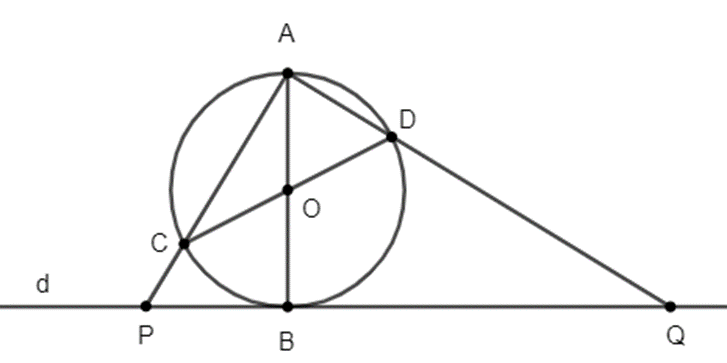
Ta có: \(\widehat {ACD} = \widehat {ABD}\)(hai góc nội tiếp cùng chắn của nửa đường tròn (O)) (1)
Lại có \(\widehat {ADB} = 90^\circ \) (Góc nội tiếp chắn nửa đường tròn)
Do đó \(\widehat {ABD} = \widehat {DQB}\) (cùng phụ \(\widehat {DBQ}\)) (2)
Từ (1) và (2) suy ra: \(\widehat {ACD} = \widehat {DQB} \Rightarrow \widehat {PCD} + \widehat {DQB} = 180^\circ \)
Suy ra tứ giác CPQD nội tiếp đường tròn.

