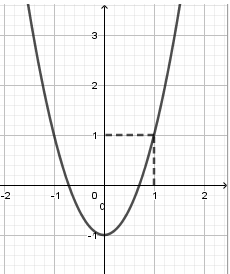
Cho hàm số bậc hai y = f(x) có đồ thị như hình vẽ bên, một hàm số g (x
Câu hỏi:
Cho hàm số bậc hai y = f(x) có đồ thị như hình vẽ bên, một hàm số g (x) xác định theo f (x) có đạo hàm . Tìm tất cả các giá trị thực của tham số m để hàm số g (x) không có cực trị.
A.
B.
C. m > 1 hoặc m < 0D
D. m > 1
Trả lời:
Đáp án B
Gọi hàm số
Đồ thị hàm số nhận điểm (0; - 1) làm đỉnh và đi qua điểm (1; 1) nên hay
Do đó
Hàm số không có cực trị vô nghiệm hoặc có nghiệm kép.
Vậy
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số . Đặt . Để đồ thị hàm số có điểm cực đại thì tổng giá trị của A + 2B là:
Xem lời giải »
Câu 2:
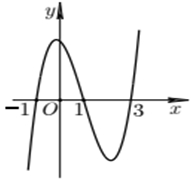
Cho hàm bậc bốn y = f(x). Hàm số y = f'(x) có đồ thị như hình bên. Số điểm cực đại của hàm số là:
Xem lời giải »
Câu 3:
Điểm thuộc đường thẳng cách đều hai điểm cực trị của đồ thị hàm số là:
Xem lời giải »
Câu 4:
Khoảng cách từ điểm cực tiểu của đồ thị hàm số đến trục tung bằng:
Xem lời giải »
Câu 5:
Cho hàm số y = f(x) có đồ thị như hình vẽ bên:
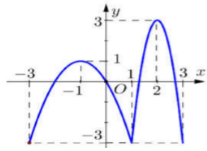
Trên đoạn , hàm số đã cho có mấy điểm cực trị?
Xem lời giải »

