Cho hàm số f(x) thỏa mãn lim x tiến tới 1+ của f(x) = âm vô cùng

Câu hỏi:

Cho hàm số f(x) thỏa mãn $\lim_{x \to 1^{+}} f (x) = - \infty$ và $\lim_{x \to 1^{-}} f (x) = 2$ . Kết luận nào sau đây đúng?

A. Đồ thị hàm số f(x) có một tiệm cận đứng là x=1.

B. Đồ thị hàm số f(x) có một tiệm cận đứng là x=2.

C. Đồ thị hàm số f(x) không có tiệm cận đứng.

D. Đồ thị hàm số f(x)có hai tiệm cận đứng là x=1 và x=2.

Trả lời:

Đáp án A

Do $\lim_{x \to 1^{+}} f (x) = - \infty$ nên đồ thị hàm số f(x) có một tiệm cận đứng là x=1

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Hàm số $y = x^{3} - 3 x^{2} - 9 x + 1$ đồng biến trên khoảng nào trong những khoảng sau?

Xem lời giải »

Câu 2:

Cho hàm số $y = \frac{x + 1}{x^{2} + 4}$ . Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là

Xem lời giải »

Câu 3:

Cho hàm số y = f(x) có bảng biến thiên như sau:

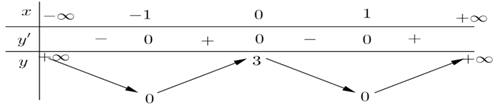
Khẳng định nào sau đây sai?

Xem lời giải »

Câu 4:

Cho hàm số y = f(x) có $\lim_{x \to 0^{+}} f (x) = + \infty, \lim_{x \to 0^{-}} f (x) = - \infty$ và $\lim_{x \to \pm \infty} f (x) = + \infty$ . Khẳng định nào sau đây là khẳng định đúng?

Xem lời giải »

Câu 5:

Đường cong sau đây là đồ thị của hàm số nào?

Xem lời giải »

Câu 6:

Cho hàm số y = f(x), có bảng biến thiên như sau:

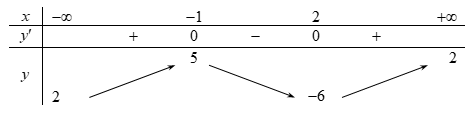
Mệnh đề nào dưới đây đúng?

Xem lời giải »

Câu 7:

Tiệm cận ngang của đồ thị hàm số $y = \frac{x + 1}{1 - 2 x}$ là:

Xem lời giải »

Câu 8:

Biết đường thẳng $y = - \frac{9}{4} x - \frac{1}{24}$ cắt đồ thị hàm số $y = \frac{x^{3}}{3} + \frac{x^{2}}{2} - 2 x$ tại một điểm duy nhất có tọa độ là $(x_{0}; y_{0})$ . Mệnh đề nào sau đây đúng?

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho hàm số f(x) thỏa mãn lim x tiến tới 1+ của f(x) = âm vô cùng

Xem thêm bài tập Toán có lời giải hay khác: