Cho hàm số f(x) = x^3 - 6x^2 + 9x. Đặt f^k(x) = f(f^(k - 1)(x)) ( với k là số tự
Câu hỏi:
Cho hàm số . Đặt (với k là số tự nhiên lớn hơn 1). Tính số nghiệm của phương trình
A. 3281
B. 3280
C. 6561
D. 6562
Trả lời:
Đáp án A
Ta có đồ thị hàm số như sau:
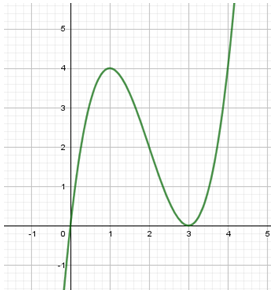
Dựa vào đồ thị hàm số ta có thể suy ra số nghiệm của phương trình f(x) = m như sau:
phương trình có 1 nghiệm duy nhất
phương trình có 2 nghiệm phân biệt
phương trình có 3 nghiệm phân biệt
Xét phương trình
Ta thấy phương trình f(x) = 0 có 2 nghiệm phân biệt, phương trình f(x) = 3 có 3 nghiệm phân biệt
Vậy phương trình có 5 nghiệm phân biệt
Xét phương trình
Phương trình có 2 + 3 nghiệm phân biệt.
Phương trình
phương trình có 9 nghiệm phân biệt
Vậy phương trình có nghiệm phân biệt (cmt)
Phương trình
Ta thấy mỗi phương trình ở trên có 9 nghiệm phân biệt nên 3 phương trình sẽ có nghiệm phân biệt.
Vậy phương trình có nghiệm.
Cứ như vậy ta tính được phương trình có nghiệm.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Với mỗi số thực x, gọi f(x) là giá trị nhỏ nhất trong các số . Giá trị lớn nhất của f(x) trên R là:
Xem lời giải »
Câu 2:
Biết rằng đồ thị của hàm số cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là . Khi đó giá trị của biểu thức bằng:
Xem lời giải »
Câu 3:
Cho hàm số y = f(x) có bảng biến thiên như sau:
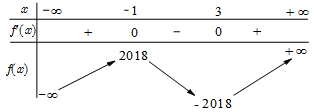
Đồ thị hàm số có bao nhiêu điểm cực trị?
Xem lời giải »
Câu 4:
Cô An đang ở khách sạn A bên bờ biển, cô cần đi du lịch đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là 10km, khoảng cách từ khách sạn A đến điểm B trên bờ gần đảo C nhất là 50km. Từ khách sạn A, cô An có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy đến hòn đảo C (như hình vẽ). Biết rằng chi phí đi đường thủy là 5USD/km, chi phí đi đường bộ là 3USD/km. Hỏi cô An phải đi đường bộ một khoảng bao nhiêu km để chi phí là nhỏ nhất.
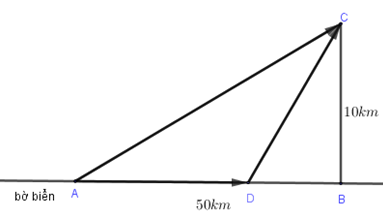
Xem lời giải »

