Câu hỏi:
Cho hàm số y = f(x) xác định trên ℝ\{−1}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ
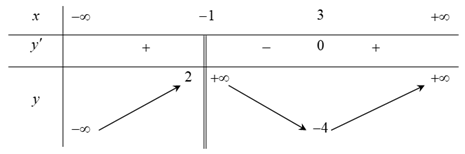
Hàm số y = |f(x)| có bao nhiêu điểm cực trị?
A. 4
B. 3
C. 2
D. 5
Trả lời:
Đáp án A
Từ bảng biến thiên của hàm số y = f(x), suy ra bảng biến thiên của hàm số y = |f(x)| là
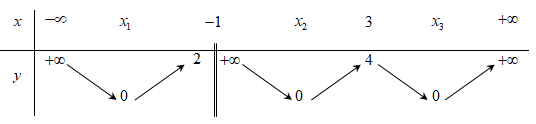
Dựa vào bảng biến thiên, ta suy ra hàm số có 4 điểm cực trị.
Câu 1:
Cho hàm số y=x+1x−1 có đồ thị là đường cong (C). M∈(C) sao cho tiếp tuyến của đồ thị hàm số tại M vuông góc với đường thẳng IM với I là tọa độ giao điểm của hai đường tiệm cận. Khi đó hoành độ của điểm M là:
Câu 2:
Tìm tất cả các giá trị của m để đường thẳng d:y=−x+m cắt đồ thị (C):y=x−12x tại 2 điểm phân biệt A, B với AB ngắn nhất?
Câu 3:
Tìm tất cả các giá trị của tham số m để hàm số y=−x3+3x2+mx+1 nghịch biến trên khoảng (0;+∞).
Câu 4:
Tìm tất cả các giá trị m để hàm số y=x3+3x2+(m+1)x+4m nghịch biến trên khoảng lớn nhất có độ dài bằng 2
Câu 5:
Cho hàm số f(x)=x3-3x2. Có bao nhiêu giá trị nguyên của m để đồ thị hàm số g(x)=f(|x|)+m cắt trục hoành tại 4 điểm phân biệt?
Câu 6:
Cho hàm số y = f(x) có đồ thị như hình dưới
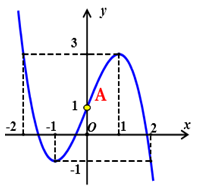
Khi đó phương trình tiếp tuyến của đồ thị hàm số tại điểm A trên hình vẽ là
Câu 7:
Cho hàm số y=f(x)=ax4+bx3+cx2+dx+e (a,b,c,d,e∈ℝ) có đồ thị như hình vẽ.
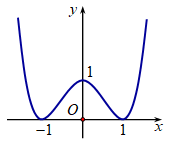
Số điểm cực trị của hàm số y=f(x2−1) là
Câu 8:
Cho hàm số y=f(x) và y=g(x) là hai hàm liên tục trên R có đồ thị hàm số y=f’(x) là đường cong nét đậm và y=g’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của y=f’(x) và y=g’(x) trên hình vẽ lần lượt có hoành độ a,b,c. Tìm giá trị nhỏ nhất của hàm số h(x)=f(x)−g(x) trên đoạn [a;c]?
