Cho hàm số y = (x - m)^3 - 3x + m^2 có đồ thị là (Cm) với m là tham số thực
Câu hỏi:
Cho hàm số y = (x – m)3 – 3x + m2 có đồ thị là (Cm) với m là tham số thực. Biết điểm M(a; b) là điểm cực đại của (Cm) ứng với một giá trị m thích hợp, đồng thời là điểm cực tiểu của (Cm) ứng với một giá trị khác của m. Tổng S = 2018a + 2020b bằng
A. 504;
B. −504;
C. 12 504;
D. 5 004.
Trả lời:
Đáp án đúng là: A
Vì điểm M(a; b) thuộc đồ thị (Cm) nên ta có:
(a – m)3 – 3a + m2 = b, \(\forall \)m ∈ ℝ (1)
Xét y’ = 3(x – m)2 – 3; y’ = 0 \( \Leftrightarrow \left[ \begin{array}{l}x = m - 1\\x = m + 1\end{array} \right.\)
Bảng biến thiên:
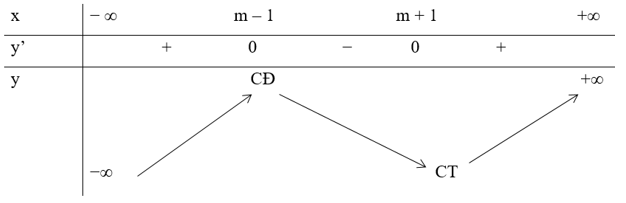
Dựa vào bảng biến thiên, ta có:
• Nếu m1 là giá trị của tham số để đồ thị hàm số nhận điểm M(a; b) là điểm cực đại thì a = m1 – 1.
• Nếu m2 là giá trị của tham số m để đồ thị hàm số nhận điểm M(a; b) là điểm cực tiểu thì a = m2 + 1
Do đó m1 = a + 1; m2 = a – 1.
Mà m1, m2 phải thỏa mãn (1) nên ta có:
\(\left\{ \begin{array}{l} - 1 - 3a + {\left( {a + 1} \right)^2} = b\\1 - 3a + {\left( {a - 1} \right)^2} = b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = \frac{{ - 1}}{4}\end{array} \right.\).
Vậy S = 2018a + 2020b = 504.

