Cho hình bình hành ABCD có M, N là trung điểm của AB, CD; AN và CM lần lượt cắt BD ở E, F. Chứng minh: a) Tứ giác AMCN là hình bình hành.
Câu hỏi:
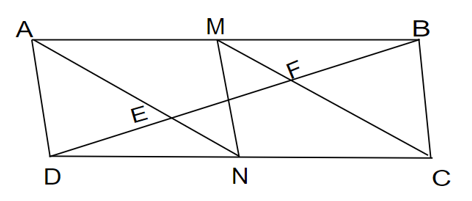
Cho hình bình hành ABCD có M, N là trung điểm của AB, CD; AN và CM lần lượt cắt BD ở E, F. Chứng minh:
a) Tứ giác AMCN là hình bình hành.
Trả lời:
a) Vì tứ giác ABCD là hình bình hành
Suy ra AB // CD, AB = CD.
Vì AB = CD mà M, N lần lượt là trung điểm AB, CD.
Suy ra AM = CN (1).
Mà AM // CN (M, N thuộc AB, CD) (2)
Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 2:
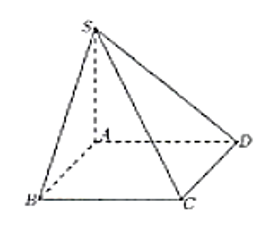
Cho hình chóp S.ABCD có đáy là hình vuông cạnh , SA vuông góc mặt phẳng đáy và SA = (minh họa hình bên). Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng?
Xem lời giải »
Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt phẳng đáy và SB = . Tính thể tích khối chóp S.ABCD?
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A, biết AC = 5 cm, AB = 6 cm và = 45°. Tính các góc , và cạnh BC (sử dụng định lí côsin)?
Xem lời giải »
Câu 6:
Một hình chữ nhật có chu vi bằng chu vi hình vuông cạnh 6cm. Chiều dài hơn chiều rộng là 6 cm .Tính diện tích hình chữ nhật đó.
Xem lời giải »
Câu 7:
Lớp 7a cuối năm chỉ có 3 loại học sinh: giỏi, khá, trung bình. Số học sinh trung bình chiếm số học sinh cả lớp. Số học sinh khá bằng 140% số học sinh giỏi. Tính số học sinh mỗi loại biết lớp 7a có 45 em.
Xem lời giải »
Câu 8:
Một miếng bìa hình chữ nhật có chiều dài 18cm và chiều dài gấp đôi chiều rộng. Hỏi diện tích miếng bìa đó bao nhiêu xăng – ti – mét vuông ?
Xem lời giải »