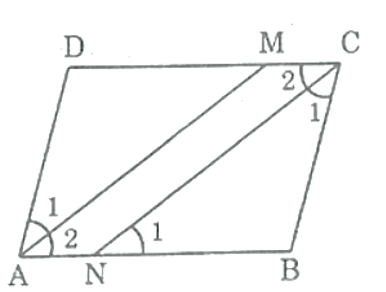
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N. Chứng minh rằng AMCN là hình bình hành.
Câu hỏi:
Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD ở M. Tia phân giác của góc C cắt AB ở N. Chứng minh rằng AMCN là hình bình hành.
Trả lời:
Ta có: ˆA=ˆC (tính chất hình bình hành)
^A2=12ˆA( Vì AM là tia phân giác của ^BAD)
^C2=12ˆC( Vì CN là tia phân giác của ^BCD )
Suy ra: ^A2= ^C2
Do ABCD là hình bình hành nên AB // CD.
Hay AN // CM (1)
Mà ^N1 = ^C2 (so le trong)
Suy ra: ^A2=^N1
⇒ AM // CN (vì có cặp góc ở vị trí đồng vị bằng nhau) (2)
Từ (1) và (2) suy ra tứ giác AMCN là hình bình hành.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho a3 + b3 + c3 = 3abc. Tính B = (1+ab)(1+bc)(1+ca) .
Xem lời giải »
Câu 2:
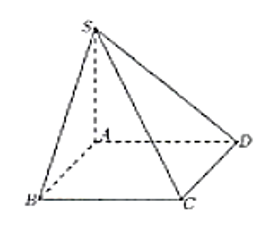
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a√3, SA vuông góc mặt phẳng đáy và SA = a√2 (minh họa hình bên). Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng?
Xem lời giải »
Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt phẳng đáy và SB = a√5 . Tính thể tích khối chóp S.ABCD?
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A, biết AC = 5 cm, AB = 6 cm và = 45°. Tính các góc ˆA , ˆC và cạnh BC (sử dụng định lí côsin)?
Xem lời giải »
Câu 5:
Cho p là số nguyên tố lớn hơn 5. Chứng minh rằng tồn tại một số có dạng 111...11 mà chia hết cho p.
Xem lời giải »
Câu 6:
Cho tam giác ABC vuông cân ở A, M là một điểm bất kỳ thuộc cạnh huyền BC. Gọi D và E theo thứ tự là hình chiếu của M trên AB và AC.
a) Tứ giác ADME là hình gì?
Xem lời giải »
Câu 7:
b) Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
Xem lời giải »
Câu 8:
Có hai hộp mỗi hộp chứa 20 quả cầu được đánh số từ 1 đến 20. Chọn ngẫu nhiên mỗi hộp 1 quả cầu. Tính xác xuất để tích số ghi trên hai quả cầu là một số chia hết cho 6.
Xem lời giải »
