Cho hình chóp S ABCD, có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB
Câu hỏi:
Cho hình chóp S ABCD, có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ A đến (SCD).
Trả lời:
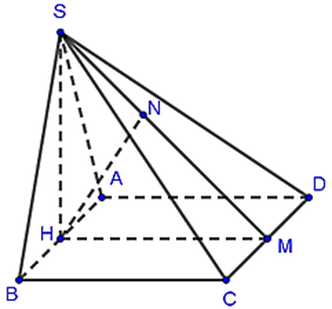
Gọi H và M lần lượt là trung điểm của AB và CD.
Tam giác SAB đều nên suy ra SH ⏊ AB.
Mà \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right.\) nên SH ⏊ (ABCD).
Kẻ HM ⏊ BD (M Î BD), kẻ HK ⏊ SM tại K.
Ta có: \[\left\{ \begin{array}{l}CD \bot HM\\CD \bot SH\;\left( {do\;SH \bot \left( {ABCD} \right)} \right)\end{array} \right.\]
\[ \Rightarrow CD \bot \left( {SHM} \right) \Rightarrow \left( {SCD} \right) \bot \left( {SHM} \right)\].
Kẻ HN ⏊ SM Þ HN ⏊ (SCD)
Do đó d(A, (SCD)) = d(H, (SCD)) = HN.
Xét tam giác SMH vuông tại H, ta có \(HM = 1;\;SH = \frac{{\sqrt 3 }}{2}\) nên
\(\frac{1}{{H{N^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{M^2}}} = \frac{1}{{{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}} + \frac{1}{{{1^2}}} = \frac{7}{3}\)
\( \Rightarrow HN = \sqrt {\frac{3}{7}} = \frac{{\sqrt {21} }}{7} \Rightarrow d\left( {A,\;\left( {SCD} \right)} \right) = d\left( {H,\;\left( {SCD} \right)} \right) = \frac{{\sqrt {21} }}{7}\).
Vậy khoảng cách từ A đến mặt phẳng (SCD) bằng \(\frac{{\sqrt {21} }}{7}\).

