Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a biết SA vuông góc với đáy, SA hợp với (SBC) một góc 45°. Tính thể tích hình chóp S.ABC.
Trả lời:
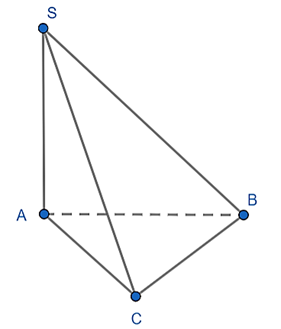
\(\widehat {SA,\left( {SBC} \right)} = \widehat {ASB} = 45^\circ \)
Suy ra: tam giác SAB vuông cân tại A
Suy ra: AS = AB = a
Thể tích khối chóp S.ABC là: VS.ABC = \(\frac{1}{3}.a.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{12}}\).
Câu 1:
Trong mặt phẳng cho 15 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng. Số tam giác có đỉnh là 3 trong số 15 điểm đã cho là?
Câu 3:
Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a ≤ 4 để X ∩ Y ≠ ∅.
Câu 4:
Làm theo mẫu: \(\frac{{143}}{{10}} = 14;\frac{3}{{10}} = 0,3\).
Yêu cầu: \(\frac{{126}}{{100}} = ...;\frac{{26}}{{100}} = ...\)
\(\frac{{1246}}{{10}} = ...;\frac{6}{{10}} = ...\)
Câu 5:
Cho đường tròn (O;R) và điểm A cố định ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên d lấy M. Qua M kẻ tiếp tuyến ME, MF với (O). Nối EF cắt OM tại H, cắt OA tại B. Chứng minh:
a) Tứ giác ABHM nội tiếp.
b) OA.OB = OH.OM = R2.
c) Tâm I của đường tròn nội tiếp tam giác MEF thuộc một đường tròn cố định khi M di chuyển trên d.
d) Tìm vị trí của M để diện tích tam giác HBO lớn nhất.
Câu 6:
Cho tam giác ABC có A’, B’, C’ lần lượt là trung điểm của BC, CA, AB.
a) Chứng minh: \(\overrightarrow {B'C'} = \overrightarrow {CA'} = \overrightarrow {A'B} \).
b) Tìm các vectơ bằng \(\overrightarrow {B'C'} ,\overrightarrow {C'A'} \).
Câu 7:
Cho tam giác ABC có A’, B’, C’ lần lượt là trung điểm của BC, CA, AB.
a) Chứng minh: \(\overrightarrow {B'C'} = \overrightarrow {CA'} = \overrightarrow {A'B} \).
b) Tìm các vectơ bằng \(\overrightarrow {B'C'} ,\overrightarrow {C'A'} \).
