Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn AB = AC = 4, góc BAC = 30 độ
Câu hỏi:
Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn AB = AC = 4, \[\widehat {BAC} = 30^\circ \]. Mặt phẳng (P) song song với (ABC) cắt đoạn SA tại M sao cho SM = 2MA. Diện tích thiết diện của (P) và hình chóp S.ABC bằng bao nhiêu?
A. \(\frac{{16}}{9}.\)
B. \(\frac{{14}}{9}.\)
C. \(\frac{{25}}{9}.\)
D. 1.
Trả lời:
Đáp án đúng là: A
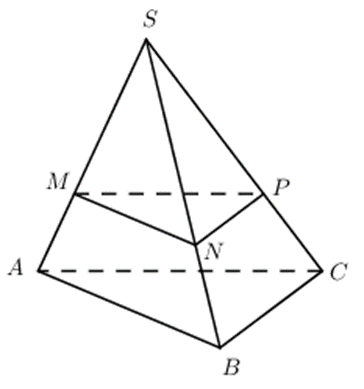
Trong ( SAB ) qua M kẻ MN // AB, trong (SAC) kẻ MP // AC.
Khi đó ta có (MNP) // (ABC).
\( \Rightarrow \left( {MNP} \right) \equiv \left( P \right){\rm{.\;}}\)
Thiết diện của (P) và hình chóp là tam giác MNP đồng dạng với tam giác ABC theo tỉ số: \(\frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3}\)
\( \Rightarrow \frac{{{S_{MNP}}}}{{{S_{ABC}}}} = {\left( {\frac{2}{3}} \right)^2} = \frac{4}{9} \Rightarrow {S_{MNP}} = \frac{4}{9}{S_{ABC}}\)
Ta có \({S_{ABC}} = \frac{1}{2}AB \cdot AC \cdot {\rm{sin}}\widehat {BAC} = \frac{1}{2} \cdot 4 \cdot 4 \cdot {\rm{sin}}30^\circ = 4\)
\( \Rightarrow {S_{MNP}} = \frac{4}{9} \cdot 4 = \frac{{16}}{9}\)
Đáp án cần chọn là: \({\rm{A}}\)

