Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm 0, cạnh AB = a
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm 0, cạnh AB = a, \(BC = a\sqrt 3 \), tam giác SAC vuông tại S. Hình chiếu vuông góc của S trên mặt phẳng đáy trùng với trung điểm H của đoạn AO. Thể tích khối chóp SABC là
A. \(\frac{{{a^3}}}{2}\);
B. \(\frac{{{a^3}}}{4}\);
C. \(\frac{{{a^3}}}{6}\);
D. \(\frac{{{a^3}}}{8}\).
Trả lời:
Đáp án đúng là: B
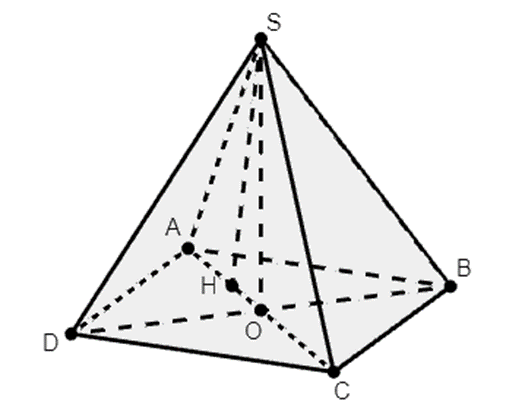
Ta có \({S_{ABC}} = \frac{1}{2}\,.\,AB\,.\,BC = \frac{{{a^2}\sqrt 3 }}{2}\).
• Xét ∆BAC vuông tại B có:
\(AC = \sqrt {A{B^2} + B{C^2}} = 2a\)
• Xét ∆SAC vuông tại S có:
\(SO = AO = \frac{{AC}}{2} = a \Rightarrow HO = \frac{{AO}}{2} = \frac{a}{2}\)
• Xét ∆SHO vuông tại H có:
\(SH = \sqrt {S{O^2} - H{O^2}} = \sqrt {{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\).
Vậy \({V_{S.ABC}} = \frac{1}{3}.{S_{ABC}}.SH = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{2}.\frac{{a\sqrt 3 }}{2} = \frac{{{a^3}}}{4}\).